I have some random test data in a 2D array of shape (500,2) as such:

xy = np.random.randint(low=0.1, high=1000, size=[500, 2])

From this array, I first select 10 random samples, to select the 11th sample, I would like to pick the sample that is the furthest away from the original 10 selected samples collectively, I am using the euclidean distance to do this. I need to keep doing this until a certain amount have been picked. Here is my attempt at doing this.

# Function to get the distance between samples
def get_dist(a, b):

    return np.sqrt(np.sum(np.square(a - b)))


# Set up variables and empty lists for the selected sample and starting samples
n_xy_to_select = 120
selected_xy = []
starting = []


# This selects 10 random samples and appends them to selected_xy
for i in range(10):
    idx = np.random.randint(len(xy))
    starting_10 = xy[idx, :]
    selected_xy.append(starting_10)
    starting.append(starting_10)
    xy = np.delete(xy, idx, axis = 0)
starting = np.asarray(starting)


# This performs the selection based on the distances
for i in range(n_xy_to_select - 1):
# Set up an empty array dists
    dists = np.zeros(len(xy))
    for selected_xy_ in selected_xy:
        # Get the distance between each already selected sample, and every other unselected sample
        dists_ = np.array([get_dist(selected_xy_, xy_) for xy_ in xy])
        # Apply some kind of penalty function - this is the key
        dists_[dists_ < 90] -= 25000
        # Sum dists_ onto dists
        dists  = dists_
    # Select the largest one
    dist_max_idx = np.argmax(dists)
    selected_xy.append(xy[dist_max_idx])
    xy = np.delete(xy, dist_max_idx, axis = 0)

The key to this is this line - the penalty function

dists_[dists_ < 90] -= 25000

This penalty function exists to prevent the code from just picking a ring of samples at the edge of the space, by artificially shortening values that are close together. However, this eventually breaks down, and the selection starts clustering, as shown in the image. You can clearly see that there are much better selections that the code can make before any kind of clustering is necessary. I feel that a kind of decaying exponential function would be best for this, but I do not know how to implement it.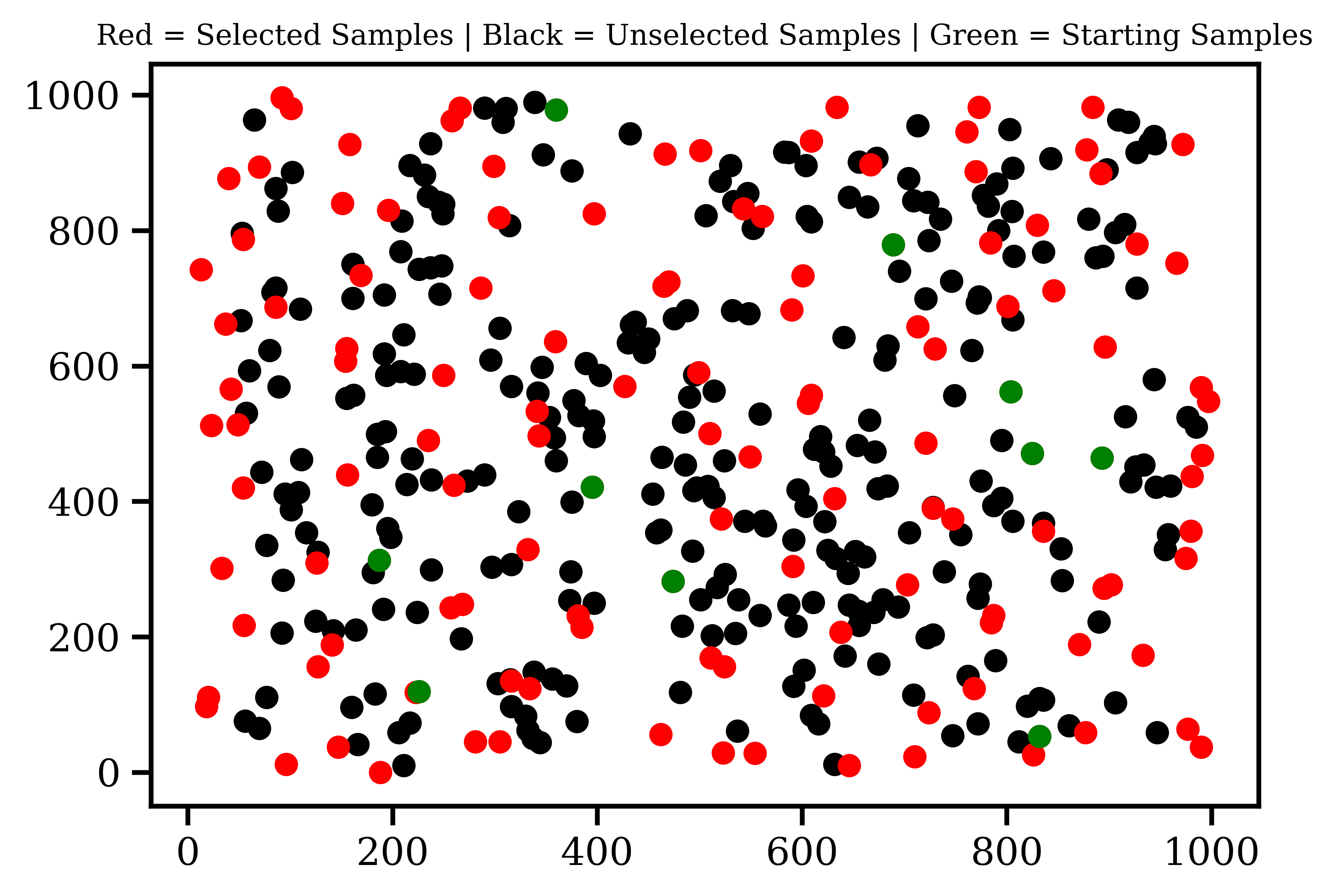 So my question is; how would I change the current penalty function to get what I'm looking for?

CodePudding user response：

From your question, I understand that what you are looking for are Periodic Boundary Conditions (PBC). Meaning that a point which at the left edge of your space is just next to the on the right end side. Thus, the maximal distance you can get along one axis is given by the half of the box (i.e. between the edge and the center).

To take into account the PBC you need to compute the distance on each axis and subtract the half of the box to that: For example, if you have a point with x1 = 100 and a second one with x2 = 900, using the PBC they are 200 units apart : |x1 - x2| - 500. In the general case, given 2 coordinates and the half size box, you end up by having:

In your case this simplifies to:

delta_x[delta_x > 500] = delta_x[delta_x > 500] - 500

To wrap it up, I rewrote your code using a new distance function (note that I removed some unnecessary for loops):

import numpy as np

def distance(p, arr, 500):
    delta_x = np.abs(p[0] - arr[:,0])
    delta_y = np.abs(p[1] - arr[:,1])
    delta_x[delta_x > 500] = delta_x[delta_x > 500] - 500
    delta_y[delta_y > 500] = delta_y[delta_y > 500] - 500
    return np.sqrt(delta_x**2   delta_y**2)

xy = np.random.randint(low=0.1, high=1000, size=[500, 2])
idx = np.random.randint(500, size=10)
selected_xy = list(xy[idx])
_initial_selected = xy[idx]
xy = np.delete(xy, idx, axis = 0)
n_xy_to_select = 120


for i in range(n_xy_to_select - 1):
    # Set up an empty array dists
    dists = np.zeros(len(xy))
    for selected_xy_ in selected_xy:
        # Compute the distance taking into account the PBC
        dists_ = distance(selected_xy_, xy)
        dists  = dists_
    # Select the largest one
    dist_max_idx = np.argmax(dists)
    selected_xy.append(xy[dist_max_idx])
    xy = np.delete(xy, dist_max_idx, axis = 0)

And indeed it creates clusters, and this is normal as you will tend to create points clusters that are at the maximal distance from each others. More than that, due to the boundary conditions, we set that the maximal distance between 2 points along one axis is given by 500. The maximal distance between two clusters is thus also 500 ! And as you can see on the image, it is the case.

More over, picking more numbers will start to draws line to connect the different clusters, starting from the central one as you can see here :

CodePudding user response：

What I was looking for is called 'Furthest Point Sampling'. I have some some more research into the solution, and the Python code used to perform this is found here: https://minibatchai.com/ai/2021/08/07/FPS.html