All binary combinations in a 2d Numpy-CodePudding

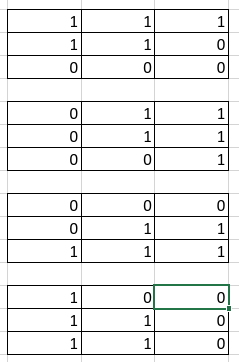
I am trying to create a code that could generate all possible combinations of 0 and 1 in a numpy matrix excluding rotations. What do I mean rotation? I mean that below matrix data are in fact the same because it has the same data but rotated 90º, 180º and 270º.

I have been trying below code but I think i am not getting all combinations and I have some of them missing. Do you have any idea if this is the right way? Do you know if there is any more efficient way?

For example, considering dx=3 and dy=3

import numpy as np

def myfunction(data)
   print(data)

dx=3
dy=3
data = np.zeros([dx, dy], dtype=np.uint8)

y=0

for x in range(dx):
    for r in range(2):
        data[x, y] = r
        myfunction(data)
        for y in range(dy):
            for s in range(2):
                data[x, y] = s
                myfunction(data)

Thank you very much!

CodePudding user response：

I am not sure if my answer is most efficient way, but anyways.

We can rotate each matrix using numpy.rot90 function.

Lets Create two different dictionaries, one to store the main matrices, the other one to store main matrices' rotations, so we can verify if a new matrix is just a rotation of previously found matrices.

def Not_Rotated(dx, dy):
    import numpy as np
    from itertools import product

    Big_Matrix = np.array([[list(i[x:x dx]) for x in range(0, len(i), dx)] for i in product("01", repeat=dx*dy)])  # Stores all possible combinations

    Main = dict()  # Stores not rotated
    Main_c = 0

    Rotations = dict()  # Stores rotated
    Rotation_c = 0

    for i in range(len(Big_Matrix)):  # Going through all combinations
        flag = 1  # A flag to check if this combination is rotated of previous ones or not. 1= is not rotated of previous ones. 0 = is rotated.
        for z in range(Rotation_c):
            if np.array_equal(Big_Matrix[i],Rotations[z]):  # Checking if this combination is rotated of previous ones or not
                flag = 0

        if flag:  # If this combination is not a rotation of previous ones
            Main[Main_c] = Big_Matrix[i]
            # Rotate it three times and store the matrices
            Rotations[Rotation_c] = np.rot90(Main[Main_c])
            Rotations[Rotation_c   1] = np.rot90(Main[Main_c])
            Rotations[Rotation_c   2] = np.rot90(Main[Main_c])
            Rotation_c  = 3
            Main_c  = 1
    return Main

CodePudding user response：

Here is a vectorized solution that can work for small matrix sizes; comments in the code illustrate a 3 by 3 case:

def get_binary_mats(n):
  # all possible n by n binary matrices up to rotation: 
  bin_mats = (np.bitwise_and(np.arange(2**(n*n))[:,None], 2 ** np.arange(n*n)) > 0)\
    .reshape(-1, n, n)
  # define a score for each matrix based on position of ones
  score = 2 ** np.arange(n*n).reshape(n,n)
  # array([[  1,   2,   4],
        #  [  8,  16,  32],
        #  [ 64, 128, 256]])
  score_arr = np.stack([np.rot90(score, k=k) for k in range(4)])
  # array([[[  1,   2,   4],
  #         [  8,  16,  32],
  #         [ 64, 128, 256]],

  #        [[  4,  32, 256],
  #         [  2,  16, 128],
  #         [  1,   8,  64]],

  #        [[256, 128,  64],
  #         [ 32,  16,   8],
  #         [  4,   2,   1]],

  #        [[ 64,   8,   1],
  #         [128,  16,   2],
  #         [256,  32,   4]]])

  scores = np.einsum("ijk,ljk->il", bin_mats, score_arr)
  _, idx = np.unique(scores.min(1), return_index=True)
  return bin_mats[idx,...]

The main idea is that we can take a "dot product" of an N by N binary matrix with an N by N matrix consisting of first N^2 powers of 2 (I call the latter the score matrix). When we do this, we get a unique integer for each possible binary matrix.

To account for rotations, we can take a "dot product" with 4 rotations of the "score" matrix, and associate each binary matrix to the minimum of the four results. We can refer to this minimum as a score of a binary matrix.

Finally, we can pick a matrix for each unique score with np.unique. For example, here is the output for n = 2:

array([[[False, False],
        [False, False]],

       [[ True, False],
        [False, False]],

       [[ True,  True],
        [False, False]],

       [[False,  True],
        [ True, False]],

       [[ True,  True],
        [ True, False]],

       [[ True,  True],
        [ True,  True]]])

As a sanity check, the number of binary matrices up to rotation lines up with this OEIS sequence for n up to 5:

%time assert [get_binary_mats(k).shape[0] for k in range(1, 6)] == [2, 6, 140, 16456, 8390720]
# takes 20 seconds on my machine