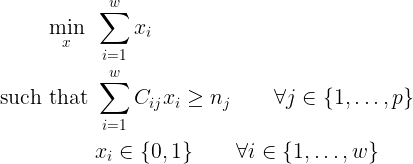I am trying to figure out an algorithm to efficiently solve the following problem:

• There are w warehouses that store p different products with different quantities
• A customer places an order on n out of the p products

The goal is to pick the minimum number of warehouses from which the order could be allocated.

E.g. the distribution of inventory in three warehouses is as follows

                |   Product 1   |   Product 2   |   Product 3   |
|---------------|---------------|---------------|---------------|
| Warehouse 1   |       2       |       5       |       0       |
| Warehouse 2   |       1       |       4       |       4       |
| Warehouse 3   |       3       |       1       |       4       |

Now suppose an order is placed with the following ordered quantities:

                |   Product 1   |   Product 2   |   Product 3   |
|---------------|---------------|---------------|---------------|
| Ordered Qty   |       5       |       4       |       1       |

The optimal solution here would be to allocate the order from Warehouse 1 and Warehouse 3. No other smaller subset of the 3 warehouses would be a better choice

I have tried using brute force to solve this, however, for a larger number of warehouses, the algorithm performs very poorly. I have also tried a few greedy allocation algorithms, however, as expected, they are unable to minimize the number of sub-orders in many cases. Are there any other algorithms/approaches that I should look into?

CodePudding user response：

Part 1 (see also Part 2 below)

Your task looks like a

Where w is the number of warehouses, p the number of products, n_j the quantity of product j ordered, and C_ij the quantity of product j stored in warehouse i. Then, the decisions are to select warehouse i (x_i = 1) or not (x_i = 0).

Using Google's ortools and the open-source CBC solver, this could be implemented as follows in Python:

import numpy as np
from ortools.linear_solver import pywraplp


# Some test data, replace with your own.
p = 50
w = 1000
n = np.random.randint(0, 10, p)
C = np.random.randint(0, 5, (w, p))

solver = pywraplp.Solver("model", pywraplp.Solver.CBC_MIXED_INTEGER_PROGRAMMING)
x = [solver.BoolVar(f"x[{i}]") for i in range(w)]
    
for j in range(p):
    solver.Add(C[:, j] @ x >= n[j])
    
solver.Minimize(sum(x))

This formulation solves instances with up to a thousand warehouses in a few seconds to a minute. Smaller instances solve much quicker, for (I hope) obvious reasons.

The following outputs the solution, and some statistics:

assert solver.Solve() is not None
    
print("Solution:")
print(f"assigned = {[i   1 for i in range(len(x)) if x[i].solution_value()]}")
print(f"     obj = {solver.Objective().Value()}")
print(f"    time = {solver.WallTime() / 1000}s")