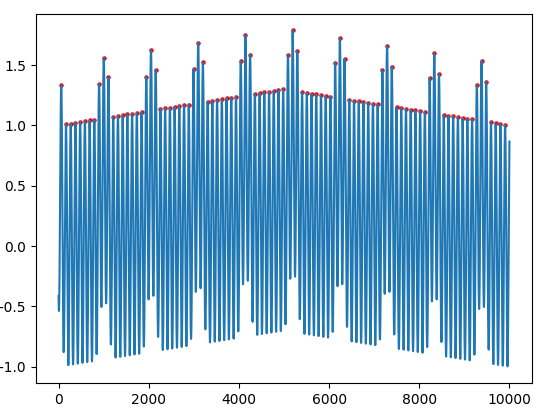
How to find series of highest peaks of a repeating pattern using find

I'm trying to determine the highest peaks of the pattern blocks in the following waveform:

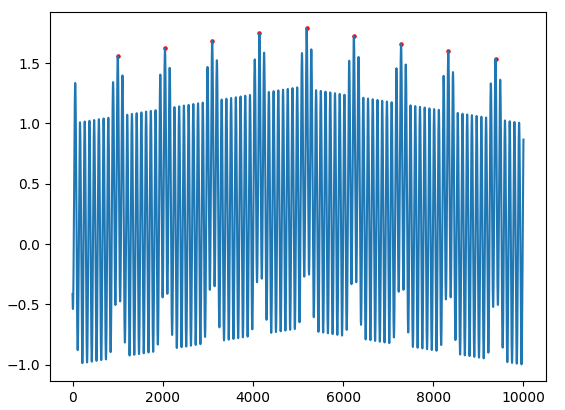
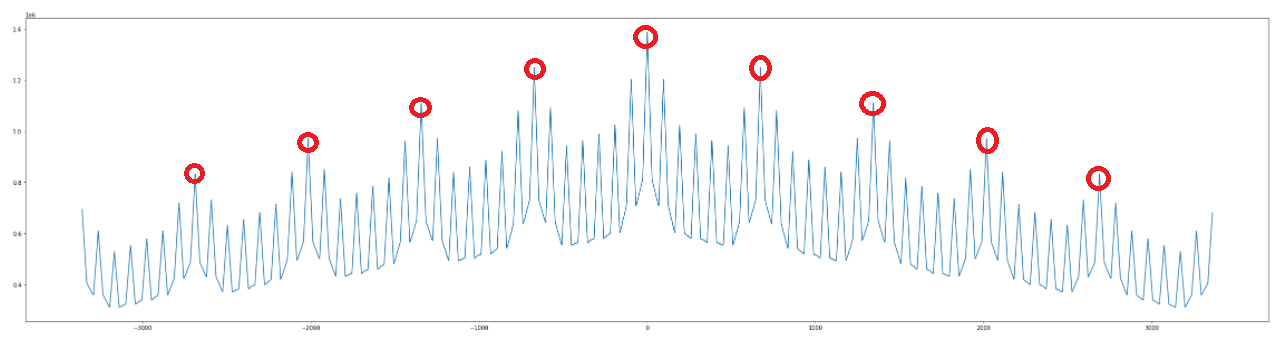
Basically, I need to detect the following peaks only (highlighted):

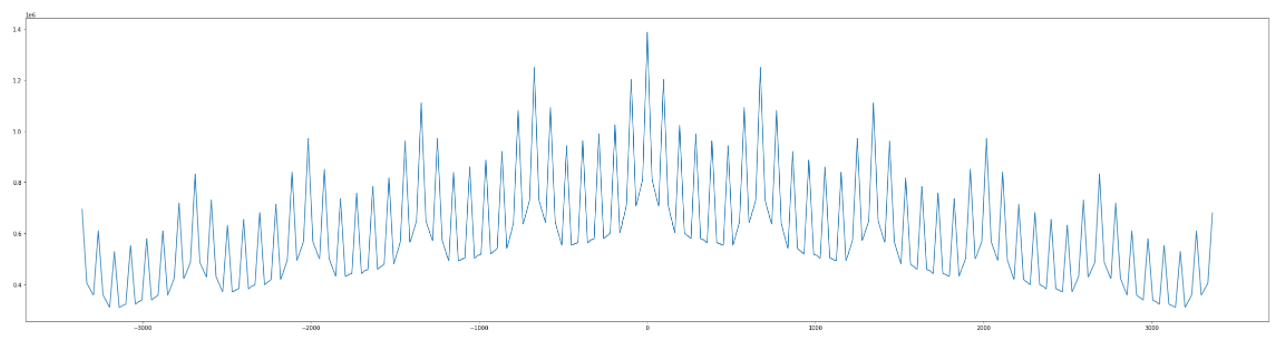
If I use scipy.find_peaks(), it's unable to detect the appropriate peaks:

indices = find_peaks(my_waveform, prominence = 1)[0]

It ends up detecting all of the following points, which is not what I am looking for:

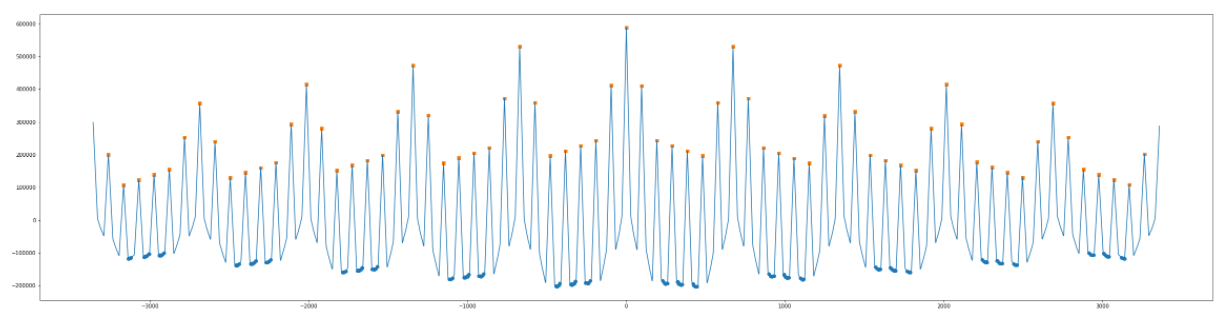
I can't provide the input arguments of distance or height thresholds to scipy.find_peaks() since there are many of the desired peaks on either extremes which are lower in height than the non-desired peaks in the middle.

Note: I had de-trended the waveform in order to aid this above problem too as you can see in the above snapshot, but it still doesn't give the right results.

So can anyone help with a correct way to tackle this?

Here's the code to fully reproduce the dataset I've shown ("autocorr" is the final waveform of interest)

import json
import sys, os
import numpy as np
import pandas as pd
import glob
import pickle

from statsmodels.tsa.stattools import adfuller, acf, pacf
from scipy.signal import find_peaks, square
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
import matplotlib.pyplot as plt

#GENERATION OF A FUNCTION WITH DUAL SEASONALITY & NOISE

def white_noise(mu, sigma, num_pts):
    """ Function to generate Gaussian Normal Noise
    Args:
        sigma: std value
        num_pts: no of points
        mu: mean value

    Returns:
        generated Gaussian Normal Noise
    """
    
    noise = np.random.normal(mu, sigma, num_pts)
    return noise

def signal_line_plot(input_signal: pd.Series, title: str = "", y_label: str = "Signal"):
    """ Function to plot a time series signal
    Args:
        input_signal: time series signal that you want to plot
        title: title on plot
        y_label: label of the signal being plotted
        
    Returns:
        signal plot
    """
    
    plt.plot(input_signal)
    plt.title(title)
    plt.ylabel(y_label)
    plt.show()

t_week = np.linspace(1,480, 480)
t_weekend=np.linspace(1,192,192)
T=96 #Time Period
x_weekday = 10*square(2*np.pi*t_week/T, duty=0.7) 10   white_noise(0, 1,480)
x_weekend = 2*square(2*np.pi*t_weekend/T, duty=0.7) 2   white_noise(0,1,192)
x_daily_weekly = np.concatenate((x_weekday, x_weekend)) 
x_daily_weekly_long = np.concatenate((x_daily_weekly,x_daily_weekly,x_daily_weekly,x_daily_weekly,x_daily_weekly,x_daily_weekly,x_daily_weekly,x_daily_weekly,x_daily_weekly,x_daily_weekly))
signal_line_plot(x_daily_weekly_long)
signal_line_plot(x_daily_weekly_long[0:1000])

#x_daily_weekly_long is the final waveform on which I'm carrying out Autocorrelation

#PERFORMING AUTOCORRELATION:
import scipy.signal as signal

autocorr = signal.correlate(x_daily_weekly_long, x_daily_weekly_long, mode = "same")
lags = signal.correlation_lags(len(x_daily_weekly_long), len(x_daily_weekly_long), mode = "same")

#VISUALIZATION:
f = plt.figure()
f.set_figwidth(40)
f.set_figheight(10)
plt.plot(lags, autocorr)

CodePudding user response：

For testing purposes i used a rough reconstruction of your signal.

import numpy as np
from scipy.signal import find_peaks, square
import matplotlib.pyplot as plt

x = np.linspace(3,103,10000)

sin = np.clip(np.sin(0.6*x)-0.5,0,10)
tri = np.concatenate([np.linspace(0,0.3,5000),np.linspace(0.3,0,5000)],axis =0)
sig = np.sin(6*x-1.2)

full = sin tri sig

peak run #1

peaks = find_peaks(full)[0]
plt.plot(full)
plt.scatter(peaks,full[peaks], color='red', s=5)
plt.show()

peak run #2 index reextraction (this needs the actual values from your signal)

peaks2 = find_peaks(full[peaks])[0]
index = peaks[peaks2]
plt.plot(full)
plt.scatter(index,full[index], color='red', s=5)
plt.show()