Recently, I came across a really interesting question:

Given the number N, how many combinations exist that can be written as the sum of several distinct squared numbers?

For example, 25 can be written as:

25 = [5**2 , 3**2   4**2]

So the answer would be 2.

But for 31, there exist no solutions, so the answer would be 0.

At the beginning, I thought this would be an easy problem to solve. I just assumed that if I count every combination of squared numbers less than square root of number N, then I should be fine, time-wise. (I found the combinations based on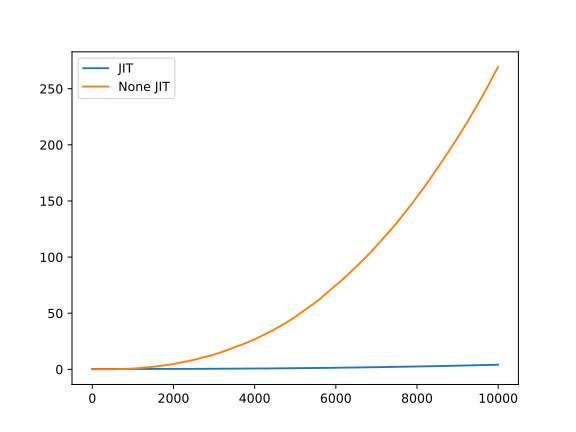

So, using JIT is significantly faster. However, this comes with a price: Numba doesn't support the bigint library and for big numbers using Numba is not valid.