Continued fraction for pi in Python-CodePudding

I'm trying to approximate pi using continued fraction.

I'm using this formula.

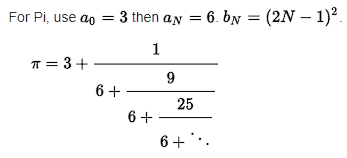
enter image description here

After many hours, I ended up here.

for i in range(1,15,1):
    e = ((2*i - 1) ** 2)
    b = (e / (6   ((2*(i 1) - 1) ** 2)))

    print(3 b)

But my output is not so great...

enter image description here

CodePudding user response：

Your approach is incorrect. If you substitute some example values in place of i you will notice that you completely disregard everything other than i-th and i 1th part of this fraction. You need to make sure that your loop takes into account all the higher levels as well as the new one you are calculating. I think the easiest way to code the solution is by using recursion:

def inf_pi(its, ctr = 1):
    if its == 0:
        return 0
    else:
        x = ((2*ctr)-1)**2 / (6   inf_pi(its - 1, ctr   1))
        return  x   (3 if ctr == 1 else 0)

print(inf_pi(10))

If you need an iterative approach, you have to consider 2 things - first of all, you can only calculate this with finite precision, and you need to replace the uncalculated remainder with some value. Second problem is that you are trying to calculate this from outermost fraction, but you don't know what the value of the "infinite" fraction is. If you reverse the order, starting form the innermost fraction, after replacing part outside of wanted precision with a constant, you can keep calculating a value for each step all the way up to the outer fraction.

def it_pi(its):
    pi = 0
    for i in range(its, 0, -1):
        pi = (((2*i)-1)**2) / (6   pi)
    return 3   pi

CodePudding user response：

Here's working Ruby code:

def pi(n)
  denom = 6.0
  n.downto(2) do |i|
    odd_sq =   (2*i-1)**2
    denom = 6.0   odd_sq / denom
  end
  return 3.0   1.0 / denom
end