Get different results when loop using more than one value-CodePudding

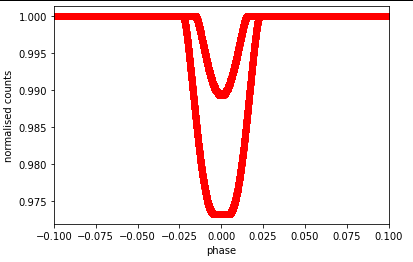
I'm trying to write a light curve simulation for transit, however, when use more than one value for the inclination ('ibound' in the code below), there will be some weird horizontal line in the final figure, but it will not happen if only one value is used each time, e.g.ibound=[80,82] is not ok, but ibound=[80] or ibound=[82] gives the correct result.

import numpy as np
import math
import matplotlib.pyplot as plt

r_p=1.314*(7.149e7)                 
r_s=0.826*(6.957e8)                 
Area_p=np.pi*r_p**2.
P=1.3*86400.
omega=2.*np.pi/P
a=0.0226*(1.496e11)


def r_cen(t):
  return a*np.sqrt( (np.sin(omega*t)**2)   (
      (np.cos(math.radians(i))**2) *
      (np.cos(omega*t)**2) ) )

def A_case2(rcen):
  Aobs = 0.
  nstep = 200
  for step in range(0,nstep):
    r=rcen-r_p (float(step)*2.*r_p/float(nstep))
    if r>r_s:
      break
    else:
      theta = ((r**2.) (rcen**2.)-(r_p**2.)) / (2.*r*rcen)
      if theta > 1.:
          theta = 1.
      Aobs=Aobs (2.*r*np.arccos(theta)*(r_p*2./float(nstep)))
  return Aobs

LC=[]
phase = []
time = []
A=[]
ibound=[80,82]
for i in ibound:
  for t in range(-int(P/5),int(P/5)):
    rcen=r_cen(float(t))
    phase.append(float(t)/P)
    time.append(float(t))
    if rcen>r_s r_p:
        A = 0.
    elif r_s>rcen r_p:
        A = Area_p
    else:
        A = A_case2(rcen)
    LC.append(1.-(A/(np.pi*r_s**2)))
    

yaxis = LC
xaxis = phase
plt.plot(xaxis,yaxis,'r',linewidth=1)
plt.xlim([-0.1,0.1])
plt.xlabel('phase')
plt.ylabel('normalised counts')
plt.show()

CodePudding user response：

Its an artifact of the plt.plot() function. As you have put all the results into the same list the plotter will attempt to connect all the data points with a single continuous line. So the end data point of the first pass will get joined to the first point of the second pass.

You can see this clearly if you change the plot parameters,

plt.plot(xaxis, yaxis, 'or', linewidth=1)

Which gives,

As you can see there has been no attempt by the plotter to connect the data points with a continuous line & hence no additional horizontal line.

CodePudding user response：

Your xaxis values have a single discontinuity halfway through, so xaxis looks something like (assuming a step size of 0.1) [-0.2, -0.1...0.1, 0.2, -0.2, -0.1...0.1, 0.2]. Like DrBwts said, this is where plt.plot connect the points across the discontinuity, resulting in a horizontal line.

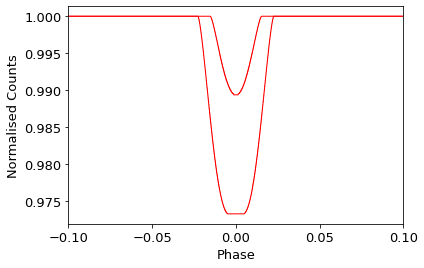
If you want the plotter to still connect data points (which is helpful if you want the graph to not look too choppy once you reduce the linewidth), you can replace the last section in your code (from yaxis = LC onwards) as follows:

yaxis = LC
xaxis = phase

num_elements_per_list = len(phase)//2

x1 = xaxis[:num_elements_per_list]
x2 = xaxis[num_elements_per_list:]

y1 = yaxis[:num_elements_per_list]
y2 = yaxis[num_elements_per_list:]

plt.plot(x1, y1, 'r', linewidth=1)
plt.plot(x2, y2, 'r', linewidth=1)
plt.xlim([-0.1,0.1])

# This line is just to make the x axis a bit prettier
plt.xticks(np.arange(-0.1, 0.101, 0.05))

plt.xlabel('Phase')
plt.ylabel('Normalised Counts')

plt.show()

This generates the following plot: