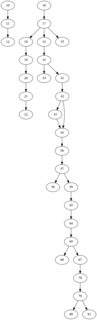
I have a data frame with parent_id and child_id columns. A snippet of the data frame is below:
df = pd.DataFrame({'child_id': [11, 12, 17, 18, 19, 20, 21, 22, 32, 33, 34, 35, 41, 42, 43, 44, 44, 56, 57, 58, 59, 63, 64, 65, 66, 67, 78, 79, 80, 81],
'parent_id': [10, 11, 16, 17, 18, 19, 20, 21, 17, 32, 33, 17, 33, 41, 42, 43, 42, 44, 56, 57, 57, 59, 63, 64, 65, 65, 67, 78, 79, 79],
})
child_id parent_id
0 11 10
1 12 11
2 17 16
3 18 17
4 19 18
...
I want to get an array that shows for each parent_id, how many steps below the children (rollout) went.
For example, for parent_id 10, there will be two elements in the returned array. The first element will have a value of 2 as it has child_id 11, and then 11 has 12. 10 also starts another rollout with child_id 20 that goes 3 steps deep. Hence, for 10 the returned array shall have 2 elements [2, 3]
The next rollout at 13 is the corner case. It produces a rollout with 4 children, one of whom (child_id: 33) produces further 4 children, one of these produces (child_id: 42) further 3. One of these (child_id: 57) starts two further rollouts. One rollout has 1 child and the other has further 6 children. So for child_id 13, I should get a rollout depth of [12, 17].
The total returned array should [2, 3, 12, 17]. I am struggling to get the corner case included in the solution.
CodePudding user response:
This is a graph problem.
Here is how your graph looks like:
If I understand correctly, you want to know the length of all possible paths from a given node to the end.
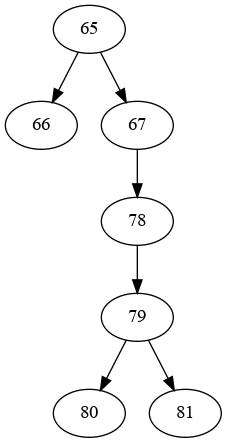
For instance, taking a subset of the graph. There are 3 possible paths from 65, of lengths 1 (to 66), 4 (to 80), and 4 (to 81).
You can use networkx to compute the graph, then determine the terminal nodes as those that do not have children using set operations. Starting fro each terminal node, go back recursively and count the edges to each given node saving the distance in a dictionary (defaultdict):
# set up graph
import networkx as nx
G = nx.from_pandas_edgelist(df, source='parent_id', target='child_id',
create_using=nx.DiGraph)
# compute paths
from collections import defaultdict
successors = defaultdict(list)
def get_parent(n, num=0):
for p in G.predecessors(n):
successors[p].append(num 1)
get_parent(p, num 1)
parents = set(df['parent_id'])
children = set(df['child_id'])
terminal = children-parents
for t in terminal:
get_parent(t)
print(dict(successors))
output:
{33: [1, 11, 10, 14, 13, 14, 13, 7, 6],
32: [2, 12, 11, 15, 14, 15, 14, 8, 7],
17: [3, 1, 13, 12, 16, 15, 16, 15, 5, 9, 8],
16: [4, 2, 14, 13, 17, 16, 17, 16, 6, 10, 9],
65: [1, 4, 4],
64: [2, 5, 5],
63: [3, 6, 6],
59: [4, 7, 7],
57: [5, 8, 8, 1],
56: [6, 9, 9, 2],
44: [7, 10, 10, 3],
43: [8, 11, 11, 4],
42: [9, 8, 12, 11, 12, 11, 5, 4],
41: [10, 9, 13, 12, 13, 12, 6, 5],
11: [1],
10: [2],
79: [1, 1],
78: [2, 2],
67: [3, 3],
21: [1],
20: [2],
19: [3],
18: [4]}
Finally, to merge to your original dataframe:
df.merge(pd.Series(successors, name='paths'),
left_on='parent_id', right_index=True)
output:
child_id parent_id paths
0 11 10 [2]
1 12 11 [1]
2 17 16 [4, 2, 14, 13, 17, 16, 17, 16, 6, 10, 9]
3 18 17 [3, 1, 13, 12, 16, 15, 16, 15, 5, 9, 8]
8 32 17 [3, 1, 13, 12, 16, 15, 16, 15, 5, 9, 8]
11 35 17 [3, 1, 13, 12, 16, 15, 16, 15, 5, 9, 8]
4 19 18 [4]
5 20 19 [3]
6 21 20 [2]
7 22 21 [1]
9 33 32 [2, 12, 11, 15, 14, 15, 14, 8, 7]
10 34 33 [1, 11, 10, 14, 13, 14, 13, 7, 6]
12 41 33 [1, 11, 10, 14, 13, 14, 13, 7, 6]
13 42 41 [10, 9, 13, 12, 13, 12, 6, 5]
14 43 42 [9, 8, 12, 11, 12, 11, 5, 4]
16 44 42 [9, 8, 12, 11, 12, 11, 5, 4]
15 44 43 [8, 11, 11, 4]
17 56 44 [7, 10, 10, 3]
18 57 56 [6, 9, 9, 2]
19 58 57 [5, 8, 8, 1]
20 59 57 [5, 8, 8, 1]
21 63 59 [4, 7, 7]
22 64 63 [3, 6, 6]
23 65 64 [2, 5, 5]
24 66 65 [1, 4, 4]
25 67 65 [1, 4, 4]
26 78 67 [3, 3]
27 79 78 [2, 2]
28 80 79 [1, 1]
29 81 79 [1, 1]
result for your 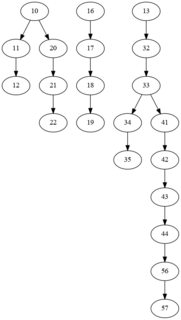
output:
child_id parent_id paths
0 11 10 [2, 3]
5 20 10 [2, 3]
1 12 11 [1]
2 17 16 [3]
3 18 17 [2]
4 19 18 [1]
6 21 20 [2]
7 22 21 [1]
8 32 13 [4, 8]
9 33 32 [3, 7]
10 34 33 [2, 6]
12 41 33 [2, 6]
11 35 34 [1]
13 42 41 [5]
14 43 42 [4]
15 44 43 [3]
16 56 44 [2]
17 57 56 [1]