Finding the numbers that make up the diagonal line in Pascal's Triangle-CodePudding

In Java, I am trying to figure out how to get the numbers that make up the diagonal lines in Pascal's triangle:

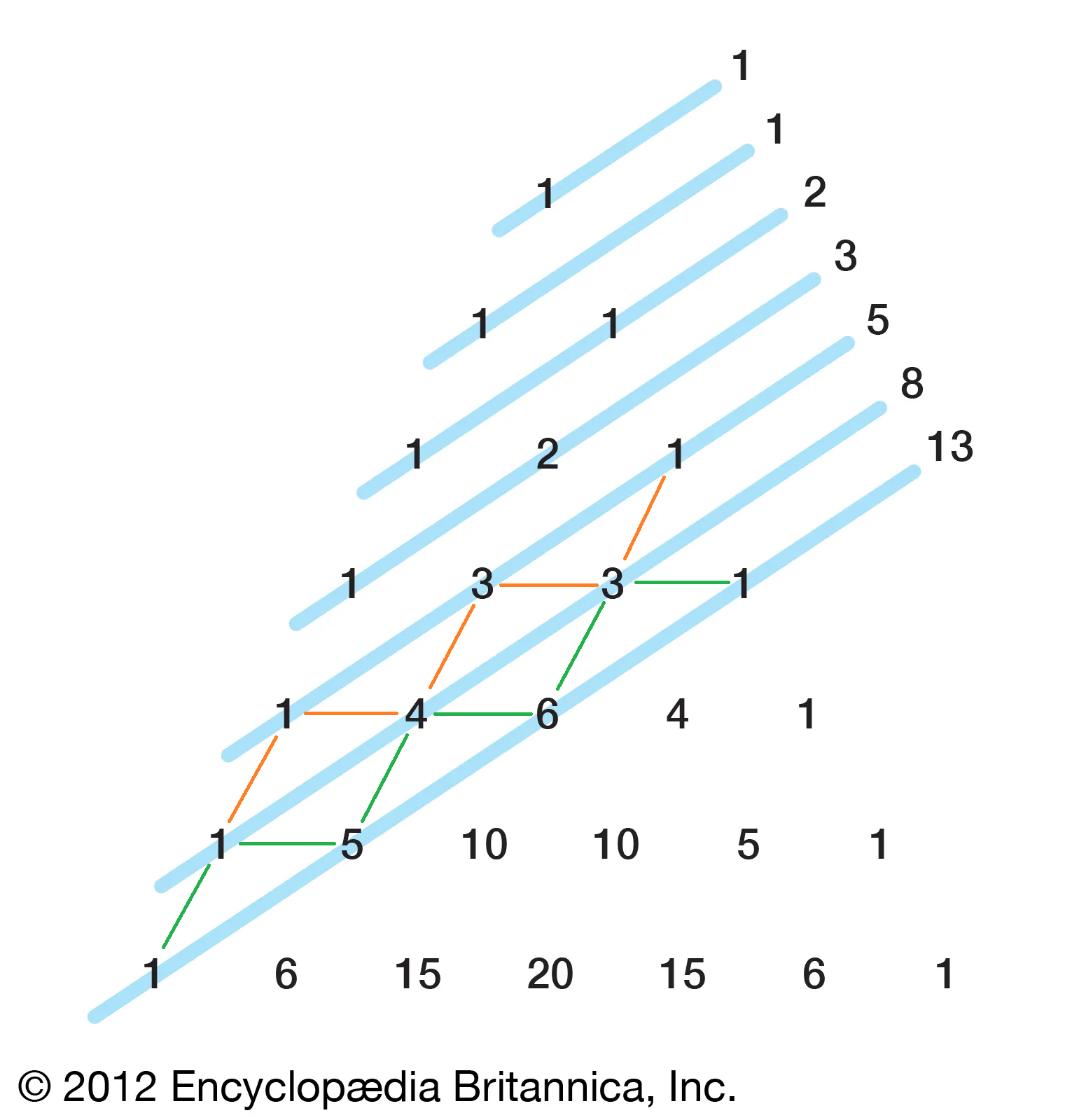
The base numbers are available for updating the values at every other index (skipping one, updating one).

So the starting point was this (orange) array:

   [1, 1, 4, 3, 3, 1]

To get the next (green) array, we prefix with a new 0, and then perform pair-wise additions from left to right:

[0, 1, 1, 4, 3, 3, 1]
 | /   | /   | /
 |/    |/    |/
[1, 1, 5, 4, 6, 3, 1]

When you need the result for a given diagonal, then you would allocate the space for this array and populate it with zeroes (instead of prepending a zero to a dynamic array/queue), and start with 1 at the right most array entry.

Then loop to apply the above logic to get to the zig-zag that includes the diagonal that you need. Finally extract the values of that diagonal, which are sitting at even indices in the zig-zag array.

Here is an implementation in a JavaScript snippet:

function pascalDiagonal(n) {
    const arr = Array(n - 1).fill(0);
    arr.push(1); // right-most value is 1 (base case - top of triangle)
    
    for (let k = n - 1; k > 0; k--)
        for (let i = k; i < n; i  = 2)
            arr[i-1]  = arr[i]; // pair wise sums
    
    // Extract the result (at even indices)
    const result = [];
    for (let i = 0; i < n; i  = 2)
        result.push(arr[i]);
    return result;
}

console.log(pascalDiagonal(7));

Note that in this implementation the argument (n) is the 1-based number of the diagonal. So adjust with 1 if you need it to be zero-based.