Accelerating FizzBuzz with numpy-CodePudding

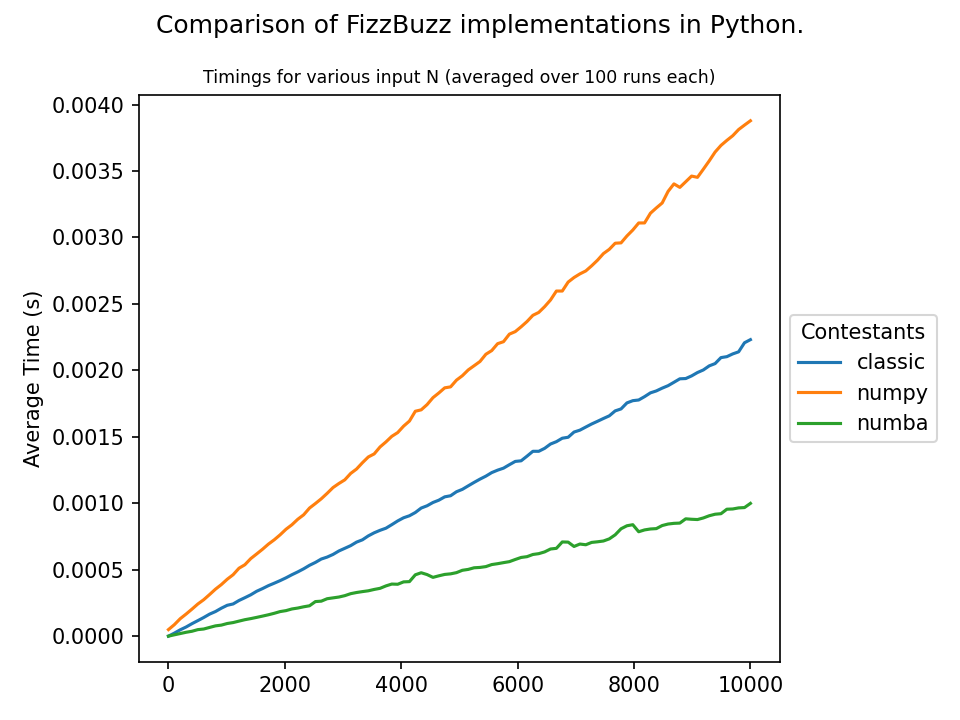
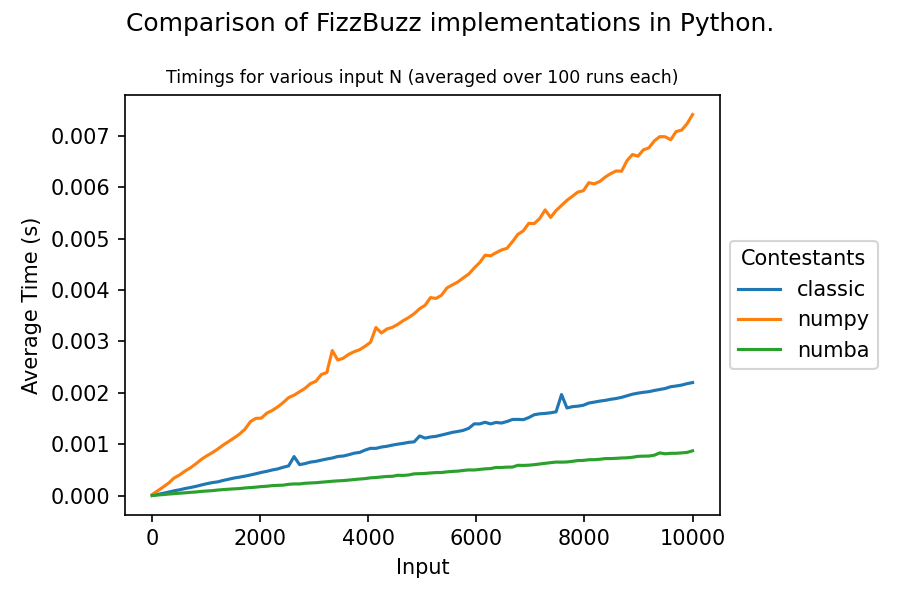
The FizzBuzz problem: Given a natural number N >= 0 print a sequence of numbers 0 - N replacing every number that is divisible by 3 with the word fizz, every number that is divisible by 5 with the word buzz, and every number divisible by both 3 and 5 with the word fizzbuzz.

Numpy isn't excellent for this (it doesn't offer much acceleration for strings), but I figured it shouldn't be too horrible and, perhaps, it can beat plain python if used wisely. To my surprise, however, the opposite is the case for a naive implementation. Why is this, and how does one improve upon this?

Here is the code that I used to generate the timings. It includes a pure-python reference implementation, a naive numpy implementation, and a numba.jit variant, because I think it can act as a reasonable lower bound on performance.

import numpy as np
import matplotlib.pyplot as plt
import numba as nb
import timeit


def classic_fizzbuzz(N: int) -> str:
    result = list()

    for idx in range(N):
        if idx % 3 == 0 and idx % 5 == 0:
            result.append("fizzbuzz")
        elif idx % 5 == 0:
            result.append("buzz")
        elif idx % 3 == 0:
            result.append("fizz")
        else:
            result.append(str(idx))

    return " ".join(result)


def numpy_fizzbuzz(N: int) -> str:
    integers = np.arange(N)
    result = np.arange(N).astype(str)
    result = np.where(integers % 3 == 0, "fizz", result)
    result = np.where(integers % 5 == 0, "buzz", result)
    result = np.where(integers % 15 == 0, "fizzbuzz", result)

    return " ".join(result)


@nb.jit(nopython=True)
def numba_fizzbuzz(N:int) -> str:
    result = list()

    for idx in range(N):
        if idx % 3 == 0 and idx % 5 == 0:
            result.append("fizzbuzz")
        elif idx % 5 == 0:
            result.append("buzz")
        elif idx % 3 == 0:
            result.append("fizz")
        else:
            result.append(str(idx))

    return " ".join(result)

# do not measure initial compile time
numba_fizzbuzz(20)

def time_fizzbuzz(fn):
    repeats = 100
    times = list()
    N_values = np.linspace(0, int(1e4), 100, dtype=int)
    for idx in N_values:
        N = int(idx)
        times.append(timeit.timeit(lambda: fn(N), number=repeats) / repeats)
    
    return N_values, times

fig, ax = plt.subplots(dpi=150)  # web-quality

contendants = {
    "classic": classic_fizzbuzz,
    "numpy": numpy_fizzbuzz,
    "numba": numba_fizzbuzz
}

for fn in contendants.values():
    ax.plot(*time_fizzbuzz(fn))

ax.set_ylabel("Average Time (s)")
ax.set_label("Input")
fig.suptitle(
    "Comparison of FizzBuzz implementations in Python.",
    # fontsize="medium",
)
ax.set_title("Timings for various input N (averaged over 100 runs each)", fontsize="small")

ax.legend(
    contendants.keys(),
    loc="center left",
    bbox_to_anchor=(1, 0.5),
    title="Contestants",
)

fig.tight_layout()

fig.savefig("timings.png")

CodePudding user response：

The reason why this happens is that you iterate all elements three times with the numpy approach. You have to check the whole array for each np.where call. The python implementation only iterates the array once. As you have shown, this is faster, although the individual steps of the iteration may be slower. That being said, you can (ab)use np.vectorize for this application, although it is explicitly not meant for the purpose of performance improvement. In that regard,