I've been trying to think of different ways to solve this problem in O(nlog n) and O(n) space complexity for a while now. I'm finding it impossible although I can easily do this in n^2.

The question is:

A salesman knows how much revenue he will get if he sells at a city for x number of days (for the entire duration from starting day to end day) and he wants to obtain as much revenue as possible in a range of days, he can only be in one city at a time. What is the maximum revenue he can obtain given the ranges of the day from input:

• City 'A', from day 1 to day 7, revenue of 5
• City 'B' from day 6 to day 9, revenue of 4
• City 'C' from day 1 to day 5, revenue of 3

Hence, to obtain the maximum revenue, he will sell from day 1 to 5 at city 'C', getting a revenue of 3 and then sell at city B day 6 to day 9, getting a revenue of 4 -> 7 in total. He is unable to sell in city B as well because its days overlap his other days in other cities

Example:

How each list is structured = [city, start_day, end_day, revenue]
rev = [['A', 1, 7, 5], ['B', 6, 9, 4], ['C', 1, 5, 3]]
>>> print(max_rev(rec))
['B', 6, 9, 4], ['C', 1, 5, 3]

My attempt for n log n:

1. Sort the list based on the last day in a city using a modified merge sort (n log n), this will get me [['C', 1, 5, 3], ['A', 1, 7, 5], ['B', 6, 9, 4]] number them 0 -> n according to its index now (I mentioned insertion sort before, I messed up as its worst case is n^2, hence I'm using merge sort now)
2. *clueless from here. Create a memo list of n (3) size and each index of memo represents the index position of a particular city in now sorted rev
3. Each index of the memo will contain the maximum revenue the salesman can obtain if he works at that city. Do this by looping through the sorted list, and for each city information, add up all the revenues between it and the cities that has a greater start_day then the selected city's end_day.

`

import math

def max_rev(rev):
    merge_sort(rev)
    memo = [math.inf] * len(rev)
    for i in range(len(rev)):
        # another for loop would mean a n^2

    return rev

rev = [['A', 1, 7, 5], ['B', 6, 9, 4], ['C', 1, 5, 3]]
print(max_rev(rev))

Here's another example I have drawn up:

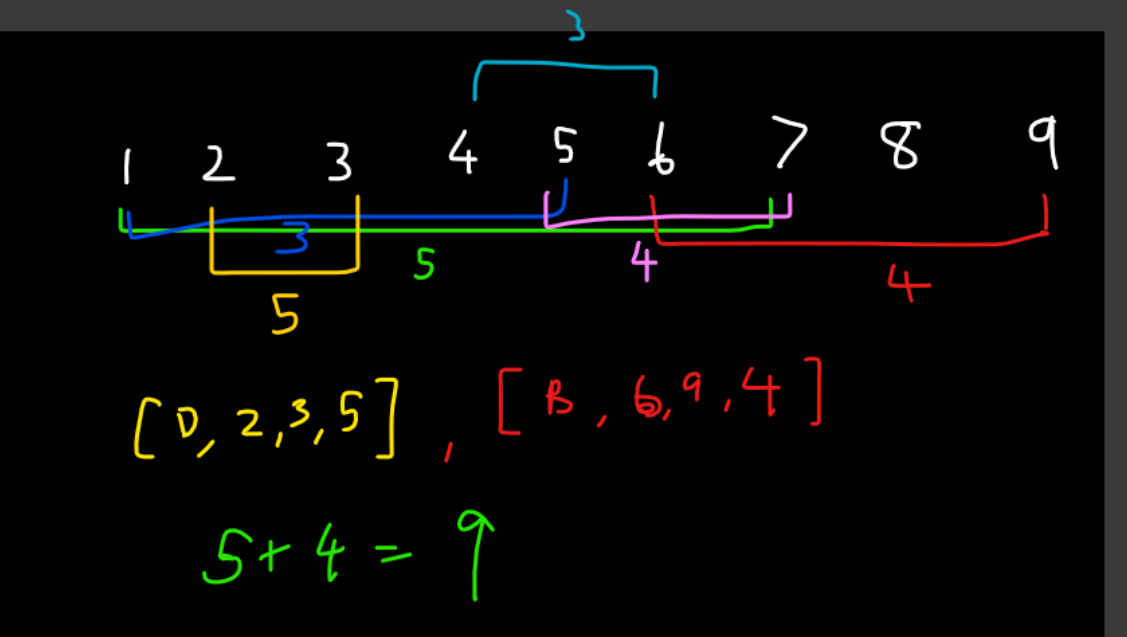
rev = [['A', 1, 7, 5], ['B', 6, 9, 4], ['C', 1, 5, 3], 
       ['D', 2, 3, 5], ['E', 5, 7, 4], ['F', 4, 6, 3]]

output -> ['D', 2, 3, 5], ['B', 6, 9, 4] 

Thanks

CodePudding user response：

You want to compare plans, not just individual cities. The important revenue is the one of the plan although the individual cities can inform our decisions.

You example allows for 2 plans: A(5) & CB(7).

In a more complex case, you could have a tree of possibilities:

start ---> A(5)
       |
       |-> B ---> C(6)
       |      |
       |      \-> D(4)
       |-> C(3)
       \-> D(1)

I'd use backtracking to find the best solution.

In this simple example, it seems that alpha-beta pruning would also immediately reduce the search space.

If you could calculate a maximum revenue per day, you could prune more aggressively.

CodePudding user response：

You made a good start. Let's begin with your sorted and numbered list of jobs.

Consider the question: "how much money can you make if you can only work jobs with numbers <= i". Call this money(i). money(n-1) is the answer you're looking for.

Obviously money(0) is the value of job 0.

money(i) for the following jobs can be easily calculated if you know the results for the previous jobs:

money(i) = max(
    money(i-1),  // this is the value if we don't do job i
    job_value(i), // this is the case when we only do job i
    job_value(i)   money(j) // j is the highest value job that ends before i starts
)

Now you just have to find the best j. The part you missed is that money(i) is always at least as big as money(i-1) -- it never hurts to have another job available, so the best job j is always the highest numbered job that ends before i starts.

Since your list of jobs is sorted by end time, you can find this job j with a binary search in O(log N) time, for O(N log N) all together.