Identifying position outliers of a moving object in a numpy array-CodePudding

I have a data set of positions (e.g. the x- or y-position of a movable object). The object moves over time, let's say linearly. The distance between consecutive positions is within a certain range (e.g. 1 /- 2.0 std). Now due to data artifacts jumps may occur, for example due to overflow some positions may jump to a whole different position which is clearly out of the ordinary.

I would like to identify the elements in my positions array that are affected by these artifacts.

Consider the following positions which grow linearly with some noise:

import numpy as np

linear_movement = np.arange(0, 100, 1)
noise = np.random.normal(loc = 0.0, scale = 2.0, size = linear_movement.size)
positions = linear_movement   noise
positions[78] = positions[78] 385

Here position 78 is affected by an artifact.

Since 'positions' is not distributed about a fixed position and data could vary over the course of the movement such that outlier positions are reached regularly later on (e.g. if I went from 0 to 1000 according to np.arange(0, 1000, 1)) I can't simply sort out positions based on a median some offset (as e.g. here: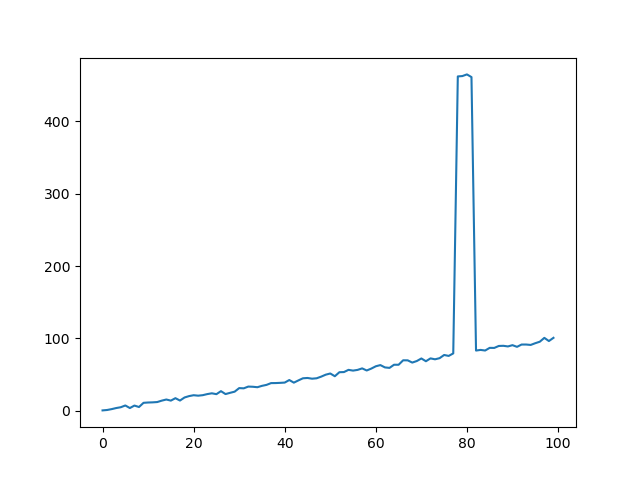

Output:

Out[264]: 
array([   0,    1,    1,    1,    2,   -3,    3,   -2,    5,    0,    0,
          0,    1,    1,   -1,    3,   -3,    4,    1,    1,    0,    0,
          1,    1,   -1,    4,   -4,    1,    1,    4,    0,    2,    0,
          0,    1,    1,    2,    0,    0,    0,    3,   -3,    3,    2,
          0,    0,    0,    2,    2,    1,   -3,    5,    0,    3,   -1,
          0,    2,   -2,    2,    3,    1,   -3,    0,    4,    0,    6,
          0,   -3,    2,    3,   -3,    3,   -1,    1,    4,   -1,    3,
        382,    0,    2,   -3, -377,    0,    0,    3,    0,    2,    0,
          0,    1,   -2,    3,    0,    0,    2,    2,    5,   -4,    4])

Things I have noted:

Every second "big number" in the distance array things in the positions array return to "normal"... (apart from special cases with positions array starting or ending with "outliers")
When there are multiple consecutive outliers, distances in between the outliers itself are inconspicuous which makes identifying them harder.

Is there a smart way or even precoded function that would take care of something like this? In my experience I am often times making the problem much more complicated than it really is ...

I could think of noting down the indices of the big numbers, take every second element (and second 1) of that indices and slice the positions array according to those... but that seems messy and again would need special cases for starting and ending with outliers.

Best

CodePudding user response：

It depends on the complexity of your data... You could look at the field of Single Particle Tracking. They developed a lot of algorithms to follow particle's trajectories, and detect outliers.

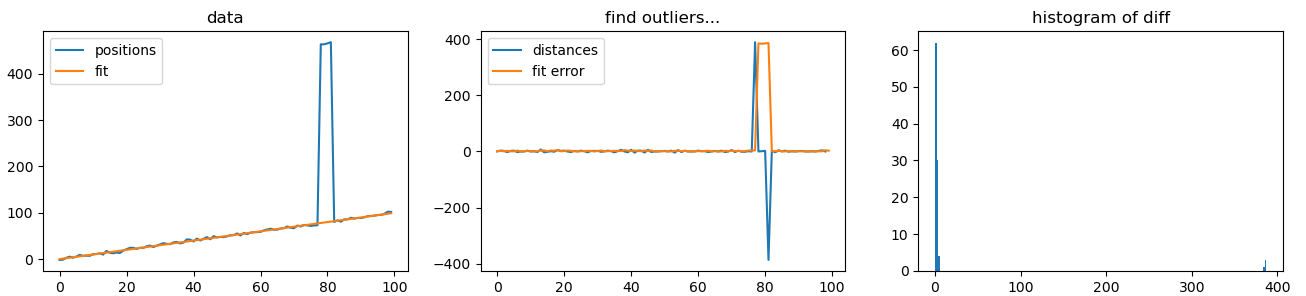
If your error often look like your example, then a simple case, you could use numpy polyfit to estimate a linear trajectories. But the fit will tend to overadjust the outliers. Then i propose to use scipy.minimize function on just an absolute norm1 (not distance but its square root). Taking the fit difference with your data really overlight the outliers. You can then use a threshold to separate them. (Otsu threshold maybe ?). This is clear on the final histogram that two groups exists.

distance = np.diff(positions).astype('int')



def to_minimize(parameter, time,position):
    return np.sum(np.abs( time*parameter[0]   parameter[1] - position))

#fit of data
time = np.arange(0,len(positions))
pfit = np.polyfit( time, positions, 1)
p0 = pfit
pfit2 = scipy.optimize.minimize( to_minimize, p0, args=(time,positions)).x
diff2 = np.abs( positions - np.polyval(pfit2, time) )
               
# 'draw'
plt.figure( figsize=(16,3.5))
plt.subplot(131)
plt.title('data')
plt.plot(positions, label='positions')
plt.plot( np.polyval(pfit2, time), label='fit')
plt.legend()
plt.subplot(132)
plt.title('find outliers...')
plt.plot( distance, label='distances')
plt.plot( np.abs( positions - np.polyval(pfit2, time)), label='fit error')
plt.legend()
plt.subplot(133)
plt.hist( diff2, bins=200 )
plt.title('histogram of difference')

CodePudding user response：

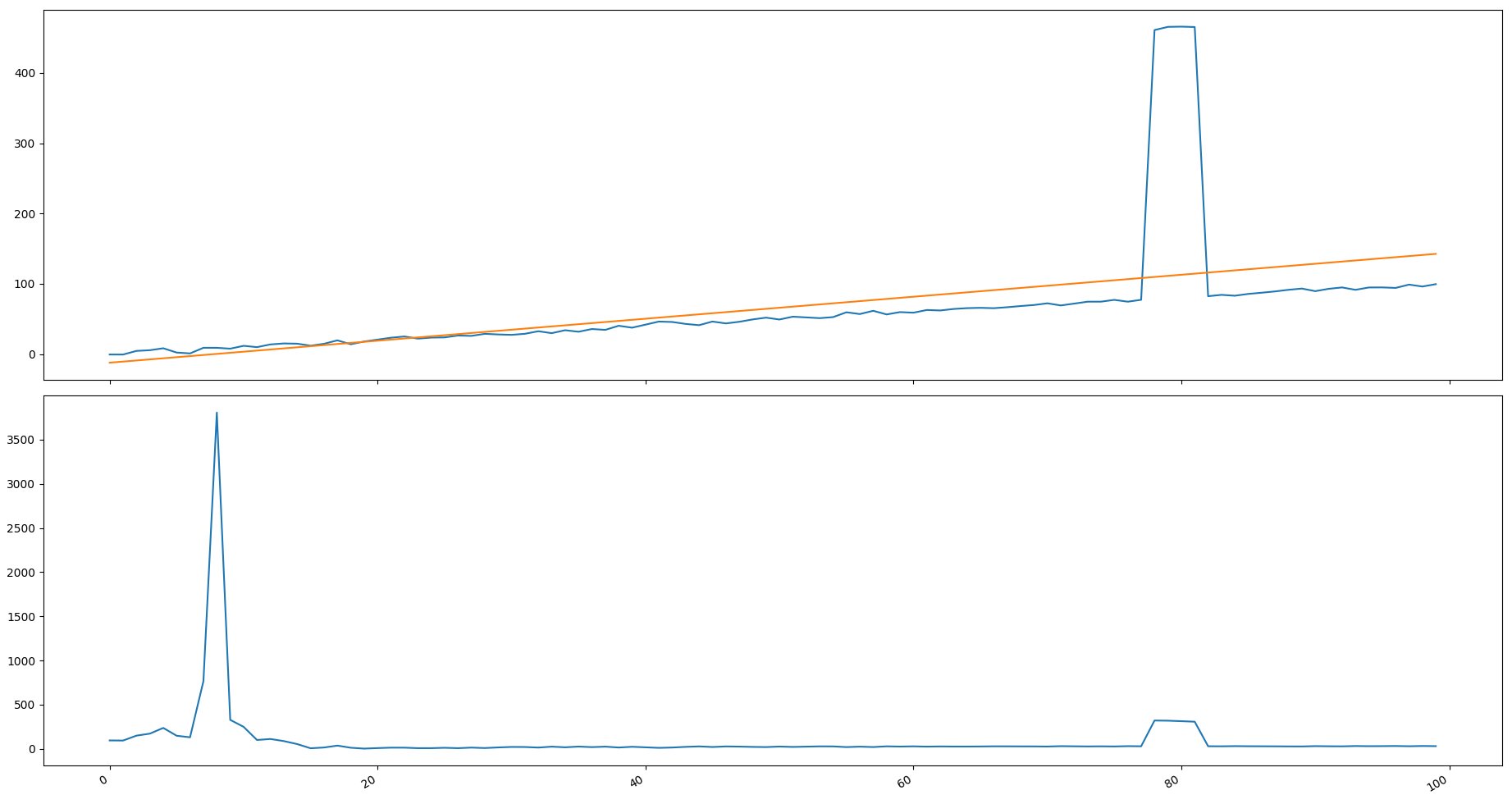
I do not pretend to answer on this topic. Just wanted to share some thoughts. Was interested in superimposing a regression line on this graph and taking the difference between the values and the regression line. Calculate deviations as a percentage. It turned out that due to the steep rise on the right, the regression line adjusted so that it went into negative values. Because of this, the difference on the left is greater than on the right. Can probably take deviations from right to left, but not more than 50% of all values.? And by the way, I like the option of the orange line proposed by Adrien Maurice more.

from sklearn.linear_model import LinearRegression
import numpy as np
import matplotlib.pyplot as plt

linear_movement = np.arange(0, 100, 1)
noise = np.random.normal(loc = 0.0, scale = 2.0, size = linear_movement.size)
positions = linear_movement   noise
positions[78:82] = positions[78:82]   385

ind = np.arange(len(positions)).reshape((-1, 1))
model = LinearRegression()
model.fit(ind, positions)
reg = model.predict(ind)
delta = (np.abs(reg - positions))/np.abs(reg/100)

fig, ax = plt.subplots(2)
ax[0].plot(ind, positions)
ax[0].plot(ind, reg)
ax[1].plot(ind, delta)

fig.autofmt_xdate()
plt.show()