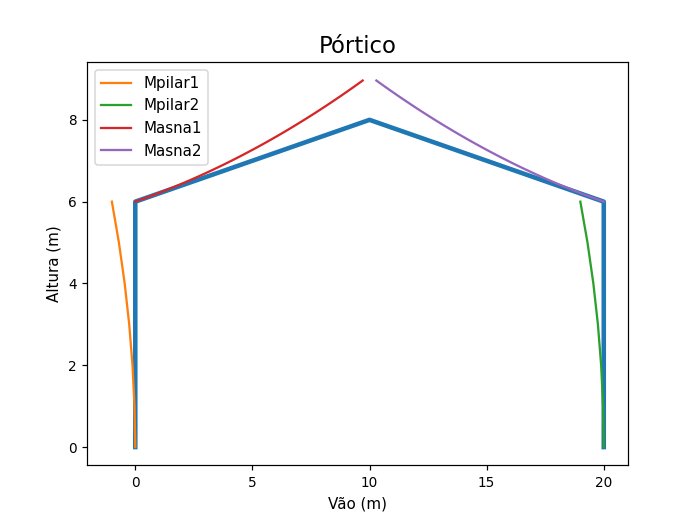
I´m a mechanical engineering student and I'm trying to create a script for moment diagram in Python. What is missing in my code is how to orientate the moment functions in order to be aligned like the portal frame.
Mpilar1 is the moment function for the fisrt column (lef to right).
Masna1 is the moment function for the fisrt beam (lef to right).
Masna2 is the moment function for the second beam (lef to right).
Mpilar2 is the moment function for the second column (lef to right).
Code:
import math as mt
import numpy as np
import warnings
import matplotlib.pyplot as plt
warnings.filterwarnings("ignore", category=np.VisibleDeprecationWarning)
#Definir parâmetros do pavilhão
v = 20 #(Vão em metros)
h = 6 #("Altura do pilar em metros:")
ht = 8 #("Altura total metros:")
alfa = (mt.atan((int(ht)-int(h))/(int(v)/2)))*180/((mt.pi))
print("Ângulo da vertente:", round(alfa, 1), "º")
lasna = ((v/2) ** 2 (ht-h) ** 2) ** 0.5
print("Comprimento de cada asna: ", round(lasna, 2), "m")
h1 = np.arange(0, h 1, 1)
ha1 = np.arange(0, lasna, 0.1)
def draw_line():
x_number_list = [0, 0, (v/2), v, v]
y_number_list = [0, h, ht, h, 0]
plt.plot(x_number_list, y_number_list, linewidth=3)
plt.title("Pórtico", fontsize=15)
plt.xlabel("Vão (m)", fontsize=10)
plt.ylabel("Altura (m)", fontsize=10)
plt.tick_params(axis='both', labelsize=9)
plt.show()
if __name__ == '__main__':
draw_line()
Mpilar1 = 1500 * h1 ** 2 350 * h1
Masna1 = 300 * ha1 ** 2 15 * ha1
Masna2 = 200 * ha1 ** 2 15 * ha1
Mpilar2 = 1400 * h1 ** 2 10 * h1
plt.plot(h1, Mpilar1)
plt.plot(ha1, Masna1)
plt.plot(ha1, Masna2)
plt.plot(h1, Mpilar2)
CodePudding user response:
You have to use transformation matrices over the points representing your curves. In particular, you'd have to use a roto-translation matrix to rotate and translate a curve to the correct position and orientation, and you might have to apply a mirror matrix to get the moments aligned according to your convention.
Please note that my structural engineering days are loooong gone, so I don't remember the convention to properly orient the moments. That's left to you as an exercise.
import math as mt
import numpy as np
import warnings
import matplotlib.pyplot as plt
warnings.filterwarnings("ignore", category=np.VisibleDeprecationWarning)
#Definir parâmetros do pavilhão
v = 20 #(Vão em metros)
h = 6 #("Altura do pilar em metros:")
ht = 8 #("Altura total metros:")
alfa_rad = mt.atan((int(ht)-int(h))/(int(v)/2))
alfa_deg = alfa_rad*180/mt.pi
print("Ângulo da vertente:", round(alfa_deg, 1), "º")
lasna = ((v/2) ** 2 (ht-h) ** 2) ** 0.5
print("Comprimento de cada asna: ", round(lasna, 2), "m")
h1 = np.arange(0, h 1, 1)
ha1 = np.arange(0, lasna, 0.1)
# Roto-translation matrix:
# Rotates the points by an angle theta and translates
# them by x in the horizontal direction, and y in the
# vertical direction
R = lambda x, y, theta: np.array([
[np.cos(theta), np.sin(theta), x],
[-np.sin(theta), np.cos(theta), y],
[0, 0, 1],
])
# mirror matrix about the x-axis
Mx = np.array([
[1, 0, 0], [0, -1, 0], [0, 0, 1]
])
# mirror matrix about the y-axis
My = np.array([
[-1, 0, 0], [0, 1, 0], [0, 0, 1]
])
Mpilar1 = 1500 * h1 ** 2 350 * h1
Masna1 = 300 * ha1 ** 2 15 * ha1
Masna2 = 200 * ha1 ** 2 15 * ha1
Mpilar2 = 1400 * h1 ** 2 10 * h1
def draw_line():
plt.figure()
x_number_list = [0, 0, (v/2), v, v]
y_number_list = [0, h, ht, h, 0]
plt.plot(x_number_list, y_number_list, linewidth=3)
# left column
points1 = np.stack([h1, Mpilar1 / max(Mpilar1), np.ones_like(h1)])
points1 = np.matmul(R(0, 0, -np.pi/2), points1)
plt.plot(points1[0, :], points1[1, :], label="Mpilar1")
# right column
points2 = np.stack([h1, Mpilar2 / max(Mpilar2), np.ones_like(h1)])
points2 = np.matmul(R(20, 0, -np.pi/2), points2)
plt.plot(points2[0, :], points2[1, :], label="Mpilar2")
# left asna
points3 = np.stack([ha1, Masna1 / max(Masna1), np.ones_like(ha1)])
points3 = np.matmul(R(0, 6, -alfa_rad), points3)
plt.plot(points3[0, :], points3[1, :], label="Masna1")
# right asna
points4 = np.stack([ha1, Masna2 / max(Masna2), np.ones_like(ha1)])
points4 = np.matmul(np.matmul(R(20, 6, alfa_rad), My), points4)
plt.plot(points4[0, :], points4[1, :], label="Masna2")
plt.title("Pórtico", fontsize=15)
plt.xlabel("Vão (m)", fontsize=10)
plt.ylabel("Altura (m)", fontsize=10)
plt.tick_params(axis='both', labelsize=9)
plt.legend()
plt.show()
draw_line()
There are a few things to note in the above code:
let's consider
points1 = np.stack([h1, Mpilar1 / max(Mpilar1), np.ones_like(h1)]). It creates a 3xn matrix of coordinates. The first row is the x-coordinates,h1. The second row is the y-coordinates of the moment,Mpilar1 / max(Mpilar1)(note that I have adimentionalized it in order to fit the chart). The third row is 1, and it is a trick to be able to apply a translation matrix. In the plot commands, we will only use the first and second rows (the x and y coordinates).points4 = np.matmul(np.matmul(R(20, 6, alfa_rad), My), points4)here I first mirrored the points about the y-axis, then I applied a rotation and translation. You will have to play in order to properly orient the moment!
CodePudding user response:
The solution works, but in this case I can´t have the correct moment diagram.
Code:
import math as mt
import numpy as np
import warnings
import matplotlib.pyplot as plt
warnings.filterwarnings("ignore", category=np.VisibleDeprecationWarning)
#Definir parâmetros do pavilhão
v = 20 #(Vão em metros)
h = 6 #("Altura do pilar em metros:")
ht = 8 #("Altura total metros:")
nm = 7 #("Número de madres por asna:")
npo = 5 #("Número de pórticos:")
dp = 5 #("Distância entre pórticos em metros:")
alfa_rad = mt.atan((int(ht)-int(h))/(int(v)/2))
alfa_deg = alfa_rad*180/mt.pi
alfa = (mt.atan((int(ht)-int(h))/(int(v)/2)))*180/((mt.pi))
print("Ângulo da vertente:", round(alfa, 1), "º")
lasna = ((v/2) ** 2 (ht-h) ** 2) ** 0.5
print("Comprimento de cada asna: ", round(lasna, 2), "m")
dm = lasna / nm
print(("Distância entre madres da cobertura em metros:"), round(dm, 2), "m")
lp = npo * dp
print("Comprimento total do pavilhão:", round(lp, 1), "m")
def draw_line():
# x axis value list.
x_number_list = [0, 0, (v/2), v, v]
# y axis value list.
y_number_list = [0, h, ht, h, 0]
# Plot the number in the list and set the line thickness.
plt.plot(x_number_list, y_number_list, linewidth=3)
# Set the line chart title and the text font size.
plt.title("Pórtico", fontsize=15)
# Set x axis label.
plt.xlabel("Vão (m)", fontsize=10)
# Set y axis label.
plt.ylabel("Altura (m)", fontsize=10)
# Set the x, y axis tick marks text size.
plt.tick_params(axis='both', labelsize=9)
# Display the plot in the matplotlib's viewer.
plt.show()
if __name__ == '__main__':
draw_line()
#EXEMPLO - IPE 100
pppilar = 8.1 #variavel do peso próprio do pilar
arpilar = 10.32 * 10 ** -4 #variavél da área de secção do pilar - m^2
inypilar = 171 * 10 ** -8 #variavél da inércia pilar segundo y - m^4
ppasna = 8.1 #variavel do peso próprio da asna
arasna = 10.32 * 10 ** -4 #variavél da área de secção do pilar - m^2
inyasna = 171 * 10 ** -8 #variavél da inércia pilar - m^4
pesomadre = 4.84 #(Peso linear das madres de cobertura em kg/m)
pesopainel = 11.2 #(Peso painel revestimento kg/m2)
rotulado = 1
base = rotulado
#Definir ações
ppcobertura = (pesopainel * dp ((pesomadre*dp)/dm) ppasna) * 9.81 / 1000 #kN/m
#print("Peso próprio da cobertura:", round(ppcobertura, 1), "kN/m")
#Sobrecarga
qk = 0.4 #Sobrecarga em kN/m2
sb = qk * dp #Sobrecarga em kN/m
#Neve
Sk = 0.5 #Neve em kN/m2
ne = Sk * dp #Neve em kN/m
#Vento
Qp1 = 0.5 #Vento pilar 1 em kN/m2
vnp1 = Qp1 * dp #Vento pilar 1 em kN/m
Qp2 = 0.5 #Vento pilar 2 em kN/m2
vnp2 = Qp2 * dp #Vento pilar 2 em kN/m
Qa1 = 0.5 #Vento asna 1 em kN/m2
vna1 = Qa1 * dp #Vento asna 1 em kN/m
Qa2 = 0.5 #Vento asna 2 em kN/m2
vna2 = Qa2 * dp #Vento asna 2 em kN/m
#Decompor as ações em normal e tagencial
ppcoberturan = ppcobertura * mt.cos(alfa*mt.pi/180)
ppcoberturat = ppcobertura * mt.sin(alfa*mt.pi/180)
sbn = sb * mt.cos(alfa*mt.pi/180) * mt.cos(alfa*mt.pi/180)
sbt = sb * mt.cos(alfa*mt.pi/180) * mt.sin(alfa*mt.pi/180)
nen = ne * mt.cos(alfa*mt.pi/180) * mt.cos(alfa*mt.pi/180)
net = ne * mt.cos(alfa*mt.pi/180) * mt.sin(alfa*mt.pi/180)
#Coeficientes de majoração
psipp = 1.35
#print("\u03A8 peso próprio:", psipp)
psi0sb = 0
#print("\u03A8 0 sobrecarga:", psi0sb)
psi1sb = 0
#print("\u03A8 1 sobrecarga:", psi1sb)
psi2sb = 0
#print("\u03A8 2 sobrecarga:", psi2sb)
ne1 = 1
ne2 = 2
nete = ne1
if nete == ne1:
psi0ne = 0.5
#print("\u03A8 0 neve:", psi0ne)
psi1ne = 0.2
#print("\u03A8 1 neve:", psi1ne)
psi2ne = 0
#print("\u03A8 2 neve:", psi2ne)
psi0vn = 0.6
#print("\u03A8 0 vento:", psi0vn)
psi1vn = 0.2
#print("\u03A8 1 vento:", psi1vn)
psi2vn = 0
#print("\u03A8 2 vento:", psi2vn)
#Combinação das ações para a cobertura - ELU - asna 1 - normal
comb_sbn = (psipp * ppcoberturan sbn * 1.5 (1.5 * psi0ne * nen 1.5 * psi0vn * vna1)) * 1000 #N/m
comb_vnn = (psipp * ppcoberturan vna1 * 1.5 (1.5 * psi0ne * nen 1.5 * sbn * psi0sb)) * 1000 #N/m
comb_nen =( psipp * ppcoberturan nen * 1.5 (1.5 * psi0vn * vna1 1.5 * sbn * psi0sb)) * 1000 #N/m
if (comb_sbn >= comb_vnn) and (comb_sbn >= comb_nen):
comb_a1n = comb_sbn
elif (comb_vnn >= comb_sbn) and (comb_vnn >= comb_nen):
comb_a1n = comb_vnn
else:
comb_a1n = comb_nen
#Combinação das ações para a cobertura - ELU - asna 1 - tangencial
comb_sbt = (psipp * ppcoberturat sbt * 1.5 (1.5 * psi0ne * net 1.5 * psi0vn * 0)) * 1000 #N/m
comb_vnt = (psipp * ppcoberturat 0 * 1.5 (1.5 * psi0ne * net 1.5 * sbt * psi0sb)) * 1000 #N/m
comb_net = (psipp * ppcoberturat net * 1.5 (1.5 * psi0vn * 0 1.5 * sbt * psi0sb)) * 1000 #N/m
if (comb_sbn >= comb_vnn) and (comb_sbn >= comb_nen):
comb_a1t = comb_sbt
elif (comb_vnn >= comb_sbn) and (comb_vnn >= comb_nen):
comb_a1t = comb_vnt
else:
comb_a1t = comb_net
#Combinação das ações para a cobertura - ELU - asna 2 - normal
comb_sb2n = (psipp * ppcoberturan sbn * 1.5 (1.5 * psi0ne * nen 1.5 * psi0vn * vna2)) * 1000 #N/m
comb_vn2n = (psipp * ppcoberturan vna2 * 1.5 (1.5 * psi0ne * nen 1.5 * sbn * psi0sb)) * 1000 #N/m
comb_ne2n = (psipp * ppcoberturan nen * 1.5 (1.5 * psi0vn * vna2 1.5 * sbn * psi0sb)) * 1000 #N/m
if (comb_sb2n >= comb_vn2n) and (comb_sb2n >= comb_ne2n):
comb_a2n = comb_sb2n
elif (comb_vn2n >= comb_sb2n) and (comb_vn2n >= comb_ne2n):
comb_a2n = comb_vn2n
else:
comb_a2n = comb_ne2n
#Combinação das ações para a cobertura - ELU - asna 2 - tangencial
comb_sbt2 = (psipp * ppcoberturat sbt * 1.5 (1.5 * psi0ne * net 1.5 * psi0vn * 0)) * 1000 #N/m
comb_vnt2 = (psipp * ppcoberturat 0 * 1.5 (1.5 * psi0ne * net 1.5 * sbt * psi0sb)) * 1000 #N/m
comb_net2 = (psipp * ppcoberturat net * 1.5 (1.5 * psi0vn * 0 1.5 * sbt * psi0sb)) * 1000 #N/m
if (comb_sb2n >= comb_vn2n) and (comb_sb2n >= comb_ne2n):
comb_a2t = comb_sbt2
elif (comb_vn2n >= comb_sb2n) and (comb_vn2n >= comb_ne2n):
comb_a2t = comb_vnt2
else:
comb_a2t = comb_net2
#Elementos finitos - Reações e deslocamentos
E = 210 * 10 ** 9 #módulo de elasticidade do aço em Pa
#Elemento 1 - asna1
a1 = E * arpilar / h
b1 = 12 * E * inypilar / h**3
c1 = 6 * E * inypilar / h**2
d1 = 4 * E * inypilar / h
e1 = 2 * E * inypilar / h
alfa1 = 90 * mt.pi / 180
l1 = mt.cos(alfa1)
m1 = mt.sin(alfa1)
t1 = np.matrix([[l1, m1, 0, 0, 0, 0],
[-m1, l1, 0, 0, 0, 0],
[0, 0 , 1, 0, 0, 0],
[0, 0, 0, l1, m1, 0],
[0, 0, 0, -m1, l1, 0],
[0 , 0, 0, 0, 0, 1]])
k1local = np.matrix([[a1, 0, 0, -a1, 0, 0],
[0, b1, c1, 0, -b1, c1],
[0, c1, d1, 0, -c1, e1],
[-a1, 0, 0, a1, 0, 0],
[0, -b1, -c1, 0, b1, -c1],
[0, c1, e1, 0, -c1, d1]])
invt1 = np.matrix.transpose(t1)
k1global = np.linalg.multi_dot([invt1, k1local, t1])
#Elmento 2 - asna 1
a2 = E * arasna / lasna
b2 = 12 * E *inyasna / lasna**3
c2 = 6 * E * inyasna / lasna**2
d2 = 4 * E * inyasna / lasna
e2 = 2 * E *inyasna / lasna
alfa2 = ((alfa) * mt.pi) / 180
l2 = mt.cos(alfa2)
m2 = mt.sin(alfa2)
t2 = np.matrix([[l2, m2, 0, 0, 0, 0],
[-m2, l2, 0, 0, 0, 0],
[0, 0 , 1, 0, 0, 0],
[0, 0, 0, l2, m2, 0],
[0, 0, 0, -m2, l2, 0],
[0 , 0, 0, 0, 0, 1]])
k2local = np.matrix([[a2, 0, 0, -a2, 0, 0],
[0, b2, c2, 0, -b2, c2],
[0, c2, d2, 0, -c2, e2],
[-a2, 0, 0, a2, 0, 0],
[0, -b2, -c2, 0, b2, -c2],
[0, c2, e2, 0, -c2, d2]])
invt2 = np.matrix.transpose(t2)
k2global = np.linalg.multi_dot([invt2, k2local, t2])
#Elmento 3 - asna 2
a3 = E * arasna / lasna
b3 = 12 * E *inyasna / lasna**3
c3 = 6 * E * inyasna / lasna**2
d3 = 4 * E * inyasna / lasna
e3 = 2 * E *inyasna / lasna
alfa3 = -alfa2
l3 = mt.cos(alfa3)
m3 = mt.sin(alfa3)
t3 = np.matrix([[l3, m3, 0, 0, 0, 0],
[-m3, l3, 0, 0, 0, 0],
[0, 0 , 1, 0, 0, 0],
[0, 0, 0, l3, m3, 0],
[0, 0, 0, -m3, l3, 0],
[0 , 0, 0, 0, 0, 1]])
k3local = np.matrix([[a3, 0, 0, -a3, 0, 0],
[0, b3, c3, 0, -b3, c3],
[0, c3, d3, 0, -c3, e3],
[-a3, 0, 0, a3, 0, 0],
[0, -b3, -c3, 0, b3, -c3],
[0, c3, e3, 0, -c3, d3]])
invt3 = np.matrix.transpose(t3)
k3global = np.linalg.multi_dot([invt3, k3local, t3])
#Elmento 4 - pilar 2
a4 = E * arpilar / h
b4 = 12 * E *inypilar / h**3
c4 = 6 * E * inypilar / h**2
d4 = 4 * E * inypilar / h
e4 = 2 * E *inypilar / h
alfa4 = -(90 * mt.pi/180)
l4 = mt.cos(alfa4)
m4 = mt.sin(alfa4)
t4 = np.matrix([[l4, m4, 0, 0, 0, 0],
[-m4, l4, 0, 0, 0, 0],
[0, 0 , 1, 0, 0, 0],
[0, 0, 0, l4, m4, 0],
[0, 0, 0, -m4, l4, 0],
[0 , 0, 0, 0, 0, 1]])
k4local = np.matrix([[a4, 0, 0, -a4, 0, 0],
[0, b4, c4, 0, -b4, c4],
[0, c4, d4, 0, -c4, e4],
[-a4, 0, 0, a4, 0, 0],
[0, -b4, -c4, 0, b4, -c4],
[0, c4, e4, 0, -c4, d4]])
invt4 = np.matrix.transpose(t4)
k4global = np.linalg.multi_dot([invt4, k4local, t4])
k = [k1global, k2global, k3global, k4global]
kportico = np.zeros([15,15])
for i,m in enumerate(k):
kportico[i*3:i*3 6,i*3:i*3 6] = m
#[K] * {U} = {F} - ELU
F12x = (comb_a1n * lasna / 2) * mt.sin((alfa*mt.pi) / 180)
F12y = (comb_a1n * lasna / 2) * mt.cos((alfa*mt.pi) / 180)
F22x = (comb_a1t * lasna / 2) * mt.cos((alfa*mt.pi) / 180)
F22y = (comb_a1t* lasna / 2) * mt.sin((alfa*mt.pi) / 180)
F13x = F12x
F13y = F12y
F23x = F22x
F23y = F22y
F33x = (comb_a2n * lasna / 2) * mt.sin((alfa*mt.pi) / 180)
F33y = (comb_a2n * lasna / 2) * mt.cos((alfa*mt.pi) / 180)
F43x = (comb_a2t * lasna / 2) * mt.cos((alfa*mt.pi) / 180)
F43y = (comb_a2t * lasna / 2) * mt.sin((alfa*mt.pi) / 180)
F14x = F33x
F14y = F33y
F24x = F43x
F24y = F43y
F1x = (vnp1 * 1000 * h) / 2
F1y = 0
M1 = -(vnp1 * 1000 * h ** 2) / 12
F2x = int((vnp1 * 1000 * h / 2) F12x - F22x)
F2y = - F12y - F22y
M2 = ((vnp1 * 1000 * h ** 2) / 12) - ((comb_a1n * lasna ** 2) / 12)
F3x = F13x - F23x - F33x F43x
F3y = -F13y - F23y - F33y - F43y
M3 = ((comb_a1n * lasna ** 2) / 12) - ((comb_a2n * lasna ** 2) / 12)
F4x = (vnp2 * h * 1000 / 2) F24x - F14x
F4y = - F14y - F24y
M4 = - ((vnp2 * 1000 * h ** 2) / 12) ((comb_a2n * lasna ** 2) / 12)
F5x = (vnp2 * 1000 * h) / 2
F5y = 0
M5 = (vnp2 * 1000 * h ** 2) / 12
f = np.array([[F1x],
[F1y],
[M1],
[F2x],
[F2y],
[M2],
[F3x],
[F3y],
[M3],
[F4x],
[F4y],
[M4],
[F5x],
[F5y],
[M5]])
fel1 = np.array([[(vnp1 * 1000 * h) / 2],
[0],
[-(vnp1 * 1000 * h ** 2) / 12],
[(vnp1 * 1000 * h) / 2],
[0],
[(vnp1 * 1000 * h ** 2) / 12]])
fel2 = np.array([[(comb_a1n * lasna / 2) * mt.sin(alfa2) - (comb_a1t * lasna / 2) * mt.cos(alfa2)],
[- (comb_a1n * lasna / 2) * mt.cos(alfa2) - (comb_a1t * lasna / 2) * mt.sin(alfa2)],
[-(comb_a1n * lasna ** 2) / 12],
[(comb_a1n * lasna / 2) * mt.sin(alfa2) - (comb_a1t * lasna / 2) * mt.cos(alfa2)],
[- (comb_a1n * lasna / 2) * mt.cos(alfa2) - (comb_a1t * lasna / 2) * mt.sin(alfa2)],
[(comb_a1n * lasna ** 2) / 12]])
fel3 = np.array([[( - comb_a2n * lasna / 2) * mt.sin(-alfa3) (comb_a2t * lasna / 2) * mt.cos(-alfa3)],
[( - comb_a2n * lasna / 2) * mt.cos(-alfa3) - (comb_a2t * lasna / 2) * mt.sin(-alfa3)],
[-(comb_a2n * lasna ** 2) / 12],
[( - comb_a2n * lasna / 2) * mt.sin(-alfa3) (comb_a2t * lasna / 2) * mt.cos(-alfa3)],
[( - comb_a2n * lasna / 2) * mt.cos(-alfa3) - (comb_a2t * lasna / 2) * mt.sin(-alfa3)],
[(comb_a2n * lasna ** 2) / 12]])
fel4 = np.array([[(vnp2 * 1000 * h) / 2],
[0],
[-(vnp2 * 1000 * h ** 2) / 12],
[(vnp2 * 1000 * h) / 2],
[0],
[(vnp2 * 1000 * h ** 2) / 12]])
if base == rotulado:
u = np.dot(np.linalg.pinv(kportico[np.ix_([2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 14], [2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 14])]), f[np.ix_([2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 14])])
utotal = np.array([[0],
[0],
[u[0]],
[u[1]],
[u[2]],
[u[3]],
[u[4]],
[u[5]],
[u[6]],
[u[7]],
[u[8]],
[u[9]],
[0],
[0],
[u[10]]])
r = np.dot(kportico, utotal) - f
rp = np.array([[r[0]],
[r[1]],
[r[12]],
[r[13]]])
rv = np.array([["R1x ="],
["R1y ="],
["R5x ="],
["R5y ="]])
uni = np.array([["N"],
["N"],
["N"],
["N"]])
size = len(rv)
print(" ")
print(" ")
if len(rv) == len(rp) and len(rv) == len(uni):
for x in range(size):
print(rv[x],rp[x],uni[x])
Fpilar1 = np.dot(k1global, utotal[0:6]) - fel1 #ESFORÇOS NÓS PILAR 1
Fasna1 = np.dot(k2global, utotal[3:9]) - fel2 #ESFORÇOS NÓS ASNA 1
Fasna2 = np.dot(k3global, utotal[6:12]) - fel3 #ESFORÇOS NÓS ASNA 2
Fpilar2 = np.dot(k4global, utotal[9:15]) - fel4 #ESFORÇOS NÓS PILAR 2
#Diagrama de esforço transverso e momentos fletores
fig, ax = plt.subplots()
h1 = np.arange(0, h 1, 1)
ha1 = np.arange(0, lasna, 0.1)
ha2 = np.arange(0, lasna, 0.1)
hp2 = np.arange(0, h 1, 1)
Mpilar1 = ((-vnp1 * 1000 * h1 ** 2 / 2) - float(Fpilar1[0]) * h1 - float(Fpilar1[2])) / 1000
Masna1 = (((- comb_a1n * ha1 ** 2 ) / 2) (float(Fasna1[1]) * mt.cos(alfa2) - float(Fasna1[0]) * mt.sin(alfa2)) * ha1 - float(Fasna1[2])) / 1000
Masna2 = (((- comb_a2n * ha2 ** 2 ) / 2) (float(Fasna2[1]) * mt.cos(alfa2) float(Fasna2[0]) * mt.sin(alfa2)) * ha2 - float(Fasna2[2])) / 1000
Mpilar2 = ((vnp2 * 1000 * hp2 ** 2 / 2) float(Fpilar2[0]) * hp2 - float(Fpilar2[2])) / 1000
# Roto-translation matrix:
# Rotates the points by an angle theta and translates
# them by x in the horizontal direction, and y in the
# vertical direction
R = lambda x, y, theta: np.array([
[np.cos(theta), np.sin(theta), x],
[-np.sin(theta), np.cos(theta), y],
[0, 0, 1],
])
# mirror matrix about the x-axis
Mx = np.array([
[1, 0, 0], [0, -1, 0], [0, 0, 1]
])
# mirror matrix about the y-axis
My = np.array([
[-1, 0, 0], [0, 1, 0], [0, 0, 1]
])
def draw_line():
plt.figure()
x_number_list = [0, 0, (v/2), v, v]
y_number_list = [0, h, ht, h, 0]
plt.plot(x_number_list, y_number_list, linewidth=3)
# left column
points1 = np.stack([h1, Mpilar1 / max(Mpilar1), np.ones_like(h1)])
points1 = np.matmul(R(0, 0, -np.pi/2), points1)
plt.plot(points1[0, :], points1[1, :], label="Mpilar1")
# right column
points2 = np.stack([h1, Mpilar2 / max(Mpilar2), np.ones_like(h1)])
points2 = np.matmul(R(20, 0, -np.pi/2), points2)
plt.plot(points2[0, :], points2[1, :], label="Mpilar2")
# left asna
points3 = np.stack([ha1, Masna1 / max(Masna1), np.ones_like(ha1)])
points3 = np.matmul(R(0, 6, -alfa_rad), points3)
plt.plot(points3[0, :], points3[1, :], label="Masna1")
# right asna
points4 = np.stack([ha1, Masna2 / max(Masna2), np.ones_like(ha1)])
points4 = np.matmul(np.matmul(R(20, 6, alfa_rad), My), points4)
plt.plot(points4[0, :], points4[1, :], label="Masna2")
plt.title("Pórtico", fontsize=15)
plt.xlabel("Vão (m)", fontsize=10)
plt.ylabel("Altura (m)", fontsize=10)
plt.tick_params(axis='both', labelsize=9)
plt.legend()
plt.show()
draw_line()