Estimate marginal effect in triple interaction-CodePudding

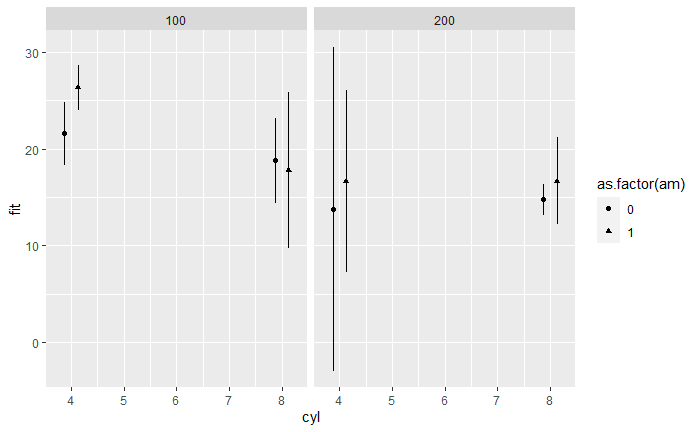
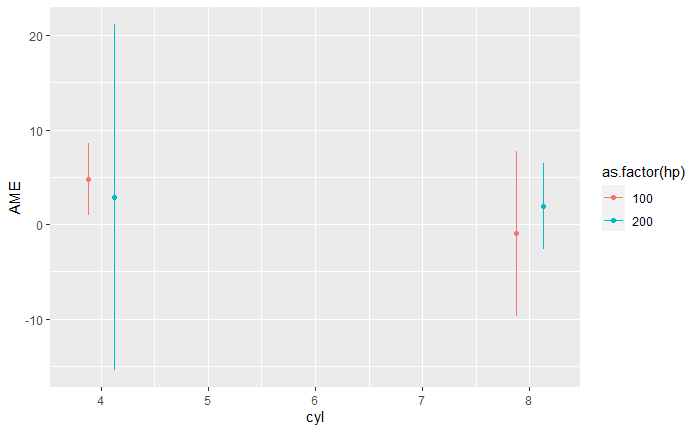
I have a model with a triple interaction, similar to this:

m1 <- lm(mpg ~ am*cyl*hp, mtcars)

I am trying to show how the effect of am changes based on the conditions of cyl and hp. Using the Effect() function from the effects library, I can show the predicted values of mpg. This works well and fairly quickly with my dataset. However, I want to show the size of the gap between the points in each case.

library(effects)
p1 <- as.data.frame(Effect(m1, focal.predictors = c("am", "cyl", "hp"), xlevels = list(am=c(0, 1), cyl=c(4,8), hp = c(100, 200))))

library(ggplot2)
ggplot(p1, aes(cyl, fit, color = as.factor(am)))  
  geom_point(position = position_dodge(0.5))  
  geom_errorbar(aes(ymin=lower, ymax=upper), width = 0, position = position_dodge(0.5))  
  facet_grid(~hp)

I have tried using the margins() function from the margins library. As shown below. This shows the average marginal effect (AME), which I suppose is what I am trying to show. However, it takes an exorbitant amount of time with my dataset because I control for country fixed effects interacted with year and one of the independent variables.

p2 <- margins(m1, at=list(cyl = c(4, 8), hp = c(100, 200)), variables = "am")
p2 <- summary(p2)

ggplot(p2, aes(cyl, AME, color = as.factor(hp)))  
  geom_point(position = position_dodge(0.5))  
  geom_errorbar(aes(ymin=lower, ymax=upper), width = 0, position = position_dodge(0.5))

Is there a way I can use Effect() to show the estimated gap between predicted values?

CodePudding user response：

All the relevant information to make the plot you want is in the output from the Effect() function. First, let's run the model and generate the effect object.

library(effects)
#> Loading required package: carData
#> lattice theme set by effectsTheme()
#> See ?effectsTheme for details.
library(ggplot2)
data(mtcars)

m1 <- lm(mpg ~ am*cyl*hp   wt   drat, mtcars)
E <- Effect(m1, 
            focal.predictors = c("am", "cyl", "hp"), 
            xlevels = list(am=c(0, 1), 
                           cyl=c(4,8), 
                           hp = seq(52, 335, length=10)))
p1 <- as.data.frame(E)

Now, to get the difference between am == 0 and am == 1, we'll need to identify those values in the data frame p1.

w0 <- which(p1$am == 0)
w1 <- which(p1$am == 1)

We can then make a matrix that we will use to generate the differences in effects. We initialize it to have all zero values and it needs to have nrow(p1) rows and length(w0) columns:

D <- matrix(0, nrow = nrow(p1), ncol = length(w0))

Now, each column corresponds to a difference between the am == 0 and am == 1 prediction for a particular value of hp and cal. For the values where am == 0, we need the matrix to have -1 values and for am == 1, we need it to have values of 1. We can accomplish this as follows:

D[cbind(w0, 1:ncol(D))] <- -1
D[cbind(w1, 1:ncol(D))] <- 1

We can then get the differences this way:

diffs <- c(t(p1$fit) %*% D)

Just to make sure we got the right numbers, let's look at the first two values of diffs:

diffs[1:2]
#> [1]  3.2716241 -0.8526864
p1[1:4, ]
#>   am cyl hp      fit       se     lower    upper
#> 1  0   4 52 24.74134 2.784239 18.967181 30.51550
#> 2  1   4 52 28.01296 2.203560 23.443061 32.58287
#> 3  0   8 52 19.12017 3.466758 11.930556 26.30979
#> 4  1   8 52 18.26749 4.455793  9.026738 27.50823
p1$fit[2]-p1$fit[1]
#> [1] 3.271624
p1$fit[4]-p1$fit[3]
#> [1] -0.8526864

You can see that the first two values of diffs are the same as the ones we would calculate from p1. Now, we need to calculate the variance of the differences, we can do this as follows:

v_diffs <- t(D) %*% vcov(E) %*% D

Next, we make a dataset that will allow us to plot these differences. We keep the data where am == 0 just so we don't have replicated rows for each comparison. Then, we add in the differences, standard errors and confidence bounds.

p11 <- p1[p1$am == 0, ]
p11$diff <- diffs
p11$se_diff <- sqrt(diag(v_diffs))
p11$lwr <- p11$diff - 1.96*p11$se_diff
p11$upr <- p11$diff   1.96*p11$se_diff

Then, we can make the plot. Now, each point represents the difference between am==0 and am==1 for each different value of hp and cyl:

ggplot(p11, aes(x=hp, y=diff, ymin=lwr, ymax=upr))   
  geom_pointrange()   
  geom_hline(yintercept=0, linetype=2, col="red")   
  facet_wrap(~as.factor(cyl))   
  theme_bw()   
  theme(panel.grid=element_blank())

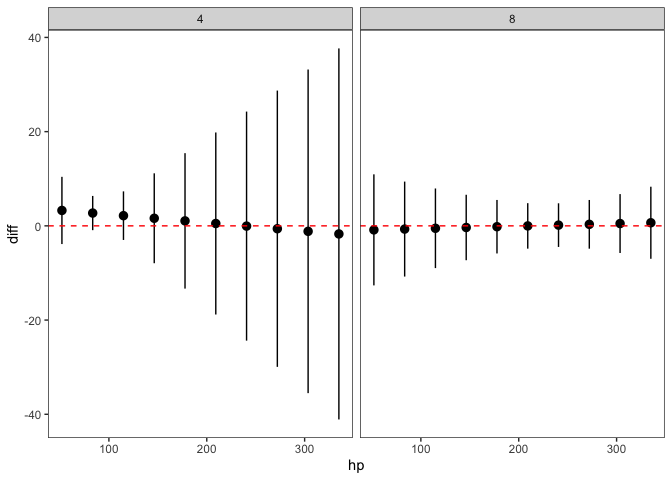
^{Created on 2022-06-01 by the reprex package (v2.0.1)}

CodePudding user response：

Here is an alternative using the marginaleffects package, which was designed as a “successor” to margins, with more flexibility, more supported model types, and is often much faster. (Disclaimer: I am the author.)

library(marginaleffects)

m <- lm(mpg ~ am*cyl*hp, mtcars)

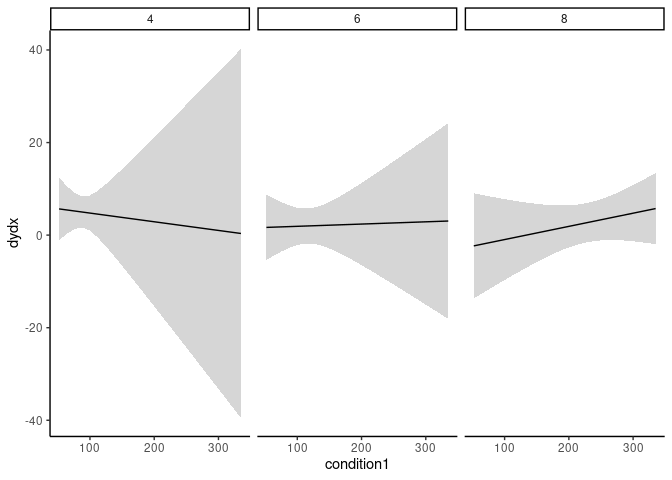
plot_cme(m, effect = "am", condition = c("hp", "cyl"))

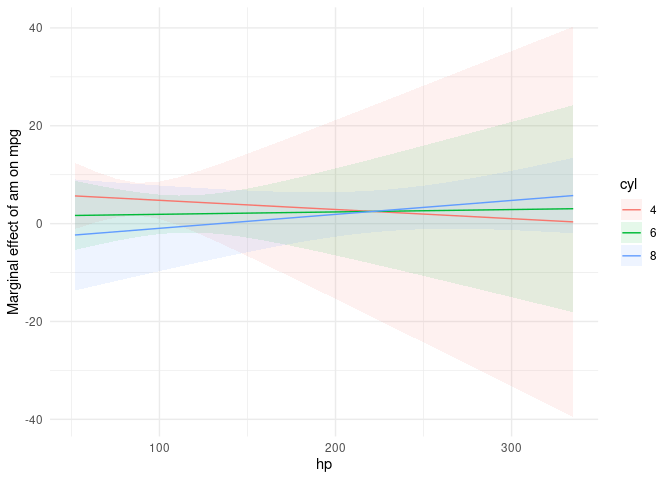
Customize the plot with ggplot2:

library(ggplot2)

plot_cme(m, effect = "am", condition = c("hp", "cyl"), draw = FALSE) |>
    ggplot(aes(condition1, dydx, ymin = conf.low, ymax = conf.high))  
    geom_ribbon(alpha = .2)  
    geom_line()  
    facet_wrap(~condition2)  
    theme_classic()

Just the numeric results:

mfx <- marginaleffects(m)
summary(mfx, by = "cyl")
#> Average marginal effects 
#>   Term cyl   Effect Std. Error z value  Pr(>|z|)    2.5 %    97.5 %
#> 1   am   6  2.00971    1.95284  1.0291 0.3034237 -1.81779  5.837211
#> 2   am   4  5.08709    1.76482  2.8825 0.0039453  1.62811  8.546073
#> 3   am   8  2.15232    2.23291  0.9639 0.3350919 -2.22410  6.528733
#> 4  cyl   6 -0.94326    0.71546 -1.3184 0.1873742 -2.34554  0.459026
#> 5  cyl   4 -2.06503    0.85842 -2.4056 0.0161455 -3.74751 -0.382553
#> 6  cyl   8  0.47177    1.71136  0.2757 0.7828002 -2.88243  3.825974
#> 7   hp   6 -0.05691    0.02592 -2.1956 0.0281202 -0.10772 -0.006108
#> 8   hp   4 -0.09174    0.03417 -2.6852 0.0072497 -0.15870 -0.024776
#> 9   hp   8 -0.03583    0.01893 -1.8930 0.0583573 -0.07293  0.001267
#> 
#> Model type:  lm 
#> Prediction type:  response