Difference of Gaussian - variable results-CodePudding

I am trying to get my head around this one. I am quite new to python and even more to image filters and manipulation. I'd like tu use OpenCV to apply this function :

 def gaussianFilter(img, kernel_size=(3,3), standard_dev=1):
    return cv2.GaussianBlur(img, ksize=kernel_size, sigmaX=standard_dev, sigmaY=standard_dev)

Later on in my code I'd want to apply a DoG. According to the definitions I've found, I could have done the following :

diff1 = gaussianFilter(img, standard_dev=1)
diff2 = gaussianFilter(img, standard_dev=10)
res = cv2.subtract(diff2,diff1)

Which should equal to using the following (from skimage.filters):

def differenceOfGaussianFilter(img,low_sigma=1, high_sigma=10):
        return difference_of_gaussians(img, low_sigma=low_sigma, high_sigma=high_sigma)

Obviously the results aren't equal. Even more, changing the parameters in gaussianFilter() doesn't change the output value much... while changing them in differenceOfGaussianFilter() render very different pictures.

My aim would be to write a simple function for differenceOfGaussianFilter() but which uses the difference between 2 gaussianFilter() calls.

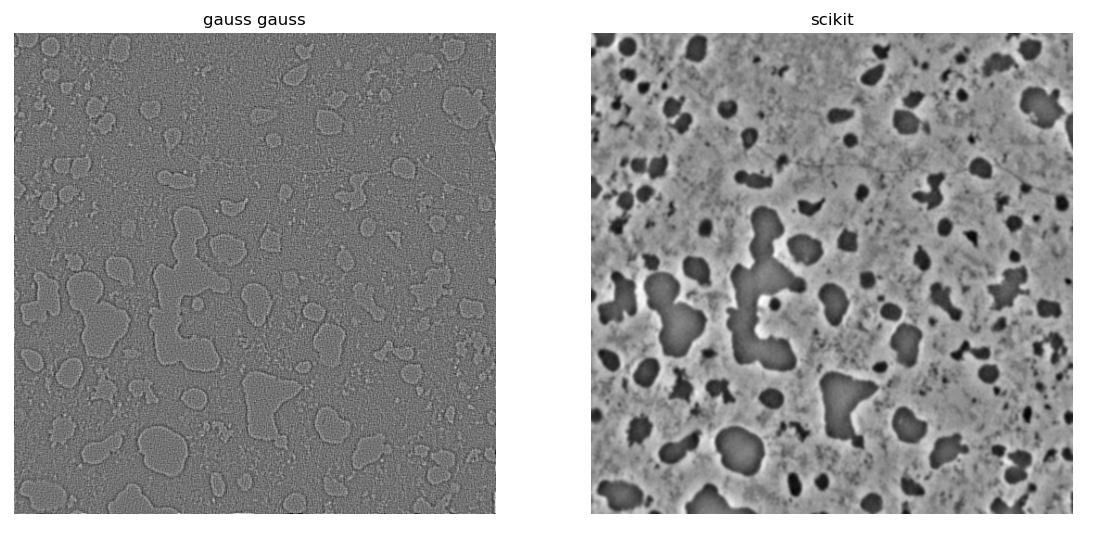
here is an example of the 2 differents results (left is gaussianFilter(10) - gaussianFilter(1) // right is differenceOfGaussianFilter(1,10) )

Any idea on how I could do that ? and why my results aren't similar ?

thanks :)

CodePudding user response：

Kernel size should be proportional to sigma.

You didn't adjust that kernel size in these calls, so your sigma=10 lowpass amounts to a 3x3 box blur... which has a sigma of around 1-2, but isn't a gaussian anymore.

Rule of thumb: kernel radius ~= 3*sigma. Then you get - three sigmas of gaussian distribution, which is 99.7% of its probability mass.

Best not give an explicit kernel size, but let cv.GaussianBlur calculate that on its own. Pass (0,0) for the size.