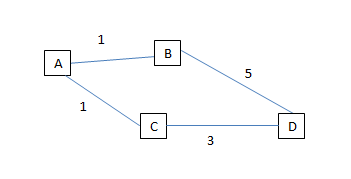
I use Dijkstra's algorithm to find the shortest path from vertex A to vertex D. But edges AB and AC have the same weight. How does Dijkstra's algorithm work if a graph has some same weight edges?

CodePudding user response：

Dijkstra's algorithm calculates the total cost from A to D, sums the weight of the edges and the best route is the one with less effort. As simple as it sounds.

if there are more than 1 routes with the same weight, then it depends of the specific implementation...

CodePudding user response：

Dijkstra's algorithm doesn't throw away possibilities -- it keeps both edge AB and edge AC "in the running". It does so by putting both B and C in the priority queue, keyed by the distance they have from node A, which is 1 in both cases. So the priority queue will give them the same priority. Depending on the implementation -- and possibly the order in which you had inserted these two nodes in that priority queue -- either B or C will be the first item in that queue. But eventually, it doesn't matter for the end result.

For instance, if B is first, then in a next cycle of the algorithm, that B will be pulled from the queue, and D is pushed unto it with a distance of 6. In a next iteration C is pulled from the queue and D gets added again to the queue (or updated -- depends on implementation), this time with distance 4. We are sure that when we pull D from the queue, it will be the version with distance 4, and so it will correctly find the shortest path.

If B was not first, but C was first, then D gets pushed into the queue with distance 4, and when B is processed, D is either rejected now (as its distance is greater than the smallest distance we have for it), or in some implementations it still gets pushed to the queue, but never reaches the front of the queue, because the other version of D (already in the queue) has a higher priority. So also in this scenario the queue will give us a D with the shortest distance, the next time we pull D from it.