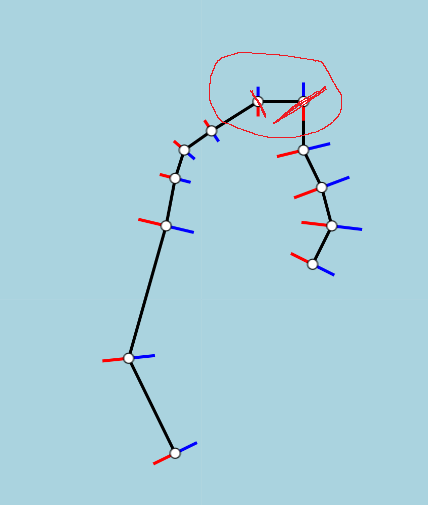
I am trying to determine the angles of the blue and red lines along the black path such that the angle of the blue and red line bisects the angle between neighboring points. To do this I have tried two different methods which both fail with the highlighted points.

The first method was to use the intersection of the two neighboring orthogonal lines that start from the midpoint of said line.

    const mP1 = { x: (p1.x   p2.x) / 2, y: (p1.y   p2.y) / 2 },
      mP2 = { x: (p2.x   p3.x) / 2, y: (p2.y   p3.y) / 2 };
    // Determining the perpendicular slopes ->  -1/slope
    const pS1 = -1 / ((p2.y - p1.y) / (p2.x - p1.x)),
      pS2 = -1 / ((p3.y - p2.y) / (p3.x - p2.x));
    // Determining the intersection of the slopes
    const j = (pS1 * (mP1.x - mP2.x) - mP1.y   mP2.y) / (pS1 - pS2);
    // point of intersection
    const iP = { x: p2.x   j, y: p2.y   j * ((pS1   pS2) / 2) };
    // determining intersecting slope
    const iS = (p2.y - iP.y) / (p2.x - iP.x);

The second method was to find the incenter of neighboring three points.

    // determining the distance of all points
    const a1 = p1.x - p2.x,
      b1 = p1.y - p2.y,
      a2 = p2.x - p3.x,
      b2 = p2.y - p3.y,
      a3 = p3.x - p1.x,
      b3 = p3.y - p1.y;
    const d1 = Math.sqrt(a1 * a1   b1 * b1),
      d2 = Math.sqrt(a2 * a2   b2 * b2),
      d3 = Math.sqrt(a3 * a3   b3 * b3);

    // point of intersection
    const iP = {
      x: (d1 * p1.x   d2 * p2.x   d3 * p3.x) / (d1   d2   d3),
      y: (d1 * p1.y   d2 * p2.y   d3 * p3.y) / (d1   d2   d3)
    };
    // determining intersecting slope
    const iS = -1 / (p2.y - iP.y) / (p2.x - iP.x);

The issue I am having is in the edge cases where the slope between two points is either 0 or undefined. In these cases, neither of the two methods that I have tried are able to produce viable slopes. Any help would be greatly appreciated, thank you.

CodePudding user response：

There are many ways to do this

Adding line normals.

This will work for any path as long as both line segments have a non zero length.

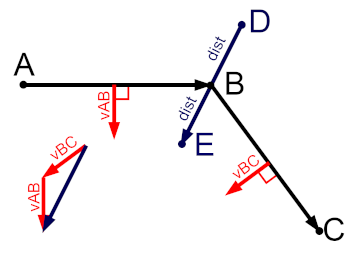
Using the following image as a reference. Arrow head denote direction of vectors.

For the path ABC to find the line DE bisecting through B

Where points A, B, C are known and represent 2D coordinates in the form {x, y}

1: Normalize the vectors AB and BC

vAB = {x: B.x -A.x, y: B.x -A.y}
vBC = {x: C.x -B.x, y: C.x -B.y}
lAB = 1.0 / Math.hypot(vAB.x, vAB.y)
vAB.x *= lAB
vAB.y *= lAB
lBC = 1.0 / Math.hypot(vBC.x, vBC.y)
vBC.x *= lBC
vBC.y *= lBC

2: Rotate both vectors 90 deg to get the normals for lines AB and BC

[vAB.x, vAB.y] = [-vAB.y, vAB.x]
[vBC.x, vBC.y] = [-vBC.y, vBC.x]

3: Add the two vectors and normalize

vDE = {x: vAB.x   vBC.x, y: vAB.y   vBC.y}
lDE = 1.0 / Math.hypot(vDE.x, vDE.y)
vDE.x *= lDE
vDE.y *= lDE

vDE is the unit vector you are looking for.

To get the line DE

• Subtract the vector vDE from point B to get point D
• Add the vector vDE to point B to get point E

(scaling where dist is distance from B of points D and E)

dist = 20
vDE.x *= dist
vDE.y *= dist
D = {x: B.x - vDE.x, y: B.y - vDE.y}
E = {x: B.x   vDE.x, y: B.y   vDE.y}