This question was closed for no reason, the provided link to a similar question does NOT provide an answer for this specific problem.
How can I have two different plots in one graph, with two separate y-axis, and with different scales?
df <- data.frame(x=3:22,
y1=c(3, 4, 5, 7, 9, 13, 15, 19, 23, 24, 29,
38, 40, 50, 56, 59, 70, 89, 104, 130),
y2=c(1,2,3,4,4,5,5,6,6,7,6,5,5,5,4,4,3,3,2,1))
ylim.prim <- c(min(df$y1), max(df$y1))
ylim.sec <- c(min(df$y2), max(df$y2))
b <- diff(ylim.prim)/diff(ylim.sec)
a <- ylim.prim[1] - b*ylim.sec[1]
ggplot(df, aes(x=x))
geom_line(aes(y=y1))
geom_line(aes(y = a y2*b))
scale_y_continuous(sec.axis = sec_axis(~ (. - a)/b))
So with this, I can plot a double y-axis, but I would like either the left or the right one to be in log-scale. Does anyone have an idea how to do that? I would like to highlight, that each axis belongs to one of the two geom_lines.
exemplary real data:
df<-structure(list(x = c(0.3499125, 8.347913, 16.34591, 24.34391,
32.34191, 40.33992, 48.33792, 56.33592, 64.33392, 72.33192, 80.32992,
88.32792, 96.32592, 104.3239, 112.3219, 120.3199, 128.3179, 136.3159,
144.3139, 152.3119, 160.3099, 168.3079, 176.3059, 184.3039, 192.3019,
200.2999, 208.2979, 216.2959, 224.2939, 232.2919, 240.2899, 248.2879,
256.2859, 264.2839, 272.2819, 280.2799, 288.2779, 296.2759, 304.2739,
312.2719, 320.2699, 328.2679, 336.2659, 344.2639, 352.2619, 360.2599,
368.2579, 376.2559, 384.2539, 392.2519, 400.2451, 408.0882, 415.9314,
423.7745, 431.7164, 439.6766, 447.6368, 455.597, 463.5572, 471.5174,
479.4776, 487.4378, 495.398, 503.3582, 511.3184, 519.2786, 527.2465,
535.234, 543.2215, 551.209, 559.1966, 567.1841, 575.1716, 583.1591,
591.1466, 599.1342, 607.1217, 615.1092, 623.0967, 631.0842, 639.0718,
647.0593, 655.0468, 663.0343, 671.0218, 679.0094, 686.9969, 694.9844,
702.9719, 710.9594, 718.947, 726.9345, 734.922, 742.9095, 750.897,
758.8846, 766.8721, 774.8596, 782.8471, 790.8346, 798.8222, 806.8097,
814.7972, 822.7847, 830.7722, 838.7598, 846.7413, 854.7015, 862.6617,
870.6219, 878.5821, 886.5423, 894.5025, 902.4627, 910.4229, 918.3831,
926.3433, 934.3035, 942.2637, 949.9737, 957.7313, 965.6915, 973.6517,
981.6119, 989.5721, 997.5323, 1005.493, 1013.453, 1021.413, 1029.373,
1037.333, 1045.294, 1053.254, 1060.905, 1068.657, 1076.5, 1084.343,
1092.245, 1100.232, 1108.22, 1116.207, 1124.195, 1132.183, 1140.17,
1148.158, 1156.145, 1164.133, 1172.12, 1180.108, 1188.095, 1196.083,
1204.07, 1212.058, 1220.045, 1228.033, 1236.02, 1244.008, 1251.995,
1259.983, 1267.97, 1275.958, 1283.945, 1291.933, 1299.92, 1307.908,
1315.895, 1323.883, 1331.871, 1339.858, 1347.846, 1355.833, 1363.821,
1371.808, 1379.796, 1387.783, 1395.771, 1403.758, 1411.683, 1419.488,
1427.293, 1435.234, 1443.214, 1451.195, 1459.175, 1467.155, 1475.135,
1483.115, 1491.095, 1499.075, 1507.055, 1515.035, 1523.015, 1530.995,
1538.975, 1546.955, 1554.935, 1562.915, 1570.895, 1578.875, 1586.855,
1594.835, 1602.815, 1610.796, 1618.776, 1626.756), y2 = c(2.27,
2.27, 2.27, 2.27, 2.27, 2.27, 2.27, 2.27, 2.27, 2.27, 2.27, 2.27,
2.27, 2.27, 2.27, 2.27, 2.27, 2.27, 2.27, 2.27, 2.27, 2.27, 2.27,
2.27, 2.27, 2.27, 2.27, 2.27, 2.27, 2.27, 2.27, 2.27, 2.27, 2.27,
2.27, 2.27, 2.27, 2.27, 2.27, 2.27, 2.27, 2.27, 2.27, 2.27, 2.27,
2.27, 2.27, 2.27, 2.27, 2.27, 2.300344, 2.300344, 2.300344, 2.300344,
2.356774, 2.356774, 2.356774, 2.356774, 2.356774, 2.356774, 2.356774,
2.356774, 2.356774, 2.356774, 2.356774, 2.356774, 2.35672, 2.35672,
2.35672, 2.35672, 2.35672, 2.35672, 2.35672, 2.35672, 2.35672,
2.35672, 2.35672, 2.35672, 2.35672, 2.35672, 2.35672, 2.35672,
2.35672, 2.35672, 2.35672, 2.35672, 2.35672, 2.35672, 2.35672,
2.35672, 2.35672, 2.35672, 2.35672, 2.35672, 2.35672, 2.35672,
2.35672, 2.35672, 2.35672, 2.35672, 2.35672, 2.35672, 2.35672,
2.35672, 2.35672, 2.35672, 2.436441, 2.436441, 2.436441, 2.436441,
2.436441, 2.436441, 2.436441, 2.436441, 2.436441, 2.436441, 2.436441,
2.436441, 2.436441, 2.593907, 2.436372, 2.436372, 2.436372, 2.436372,
2.436372, 2.436372, 2.436372, 2.436372, 2.436372, 2.436372, 2.436372,
2.436372, 2.436372, 2.32186, 2.362217, 2.362217, 2.362217, 2.356666,
2.356666, 2.356666, 2.356666, 2.356666, 2.356666, 2.356666, 2.356666,
2.356666, 2.356666, 2.356666, 2.356666, 2.356666, 2.356666, 2.356666,
2.356666, 2.356666, 2.356666, 2.356666, 2.356666, 2.356666, 2.356666,
2.356666, 2.356666, 2.356666, 2.356666, 2.356666, 2.356666, 2.356666,
2.356666, 2.356666, 2.356666, 2.356666, 2.356666, 2.356666, 2.356666,
2.356666, 2.356666, 2.356666, 2.356666, 2.6, 2.6, 2.6, 1.38,
1.38, 1.38, 1.38, 1.38, 1.38, 1.38, 1.38, 1.38, 1.38, 1.38, 1.38,
1.38, 1.38, 1.38, 1.38, 1.38, 1.38, 1.38, 1.38, 1.38, 1.38, 1.38,
1.38, 1.38), y1 = c(1.0121711505181e-12, 1.36703949435522e-12,
1.84632494858934e-12, 2.49364868526704e-12, 3.36792573591631e-12,
4.54872499912722e-12, 6.14351261535188e-12, 8.29743536886833e-12,
1.12065270336094e-11, 1.5135549574501e-11, 2.04420900737953e-11,
2.76091094527446e-11, 3.7288908764166e-11, 5.03624430409839e-11,
6.80195634790675e-11, 9.1867308143082e-11, 1.24076096081818e-10,
1.67577290537946e-10, 2.26330068874485e-10, 3.05681854075198e-10,
4.12854243103824e-10, 5.57601379152127e-10, 7.53097024416113e-10,
1.01713383727135e-09, 1.37374208059794e-09, 1.85537854367786e-09,
2.50587585968424e-09, 3.38443865549292e-09, 4.57102650080046e-09,
6.17363418887535e-09, 8.33811836170825e-09, 1.12614720154805e-08,
1.52097587979964e-08, 2.05423179929812e-08, 2.77444811472099e-08,
3.74717262176886e-08, 5.06093638045714e-08, 6.83530636095683e-08,
9.23177269923811e-08, 1.24684445803943e-07, 1.68399029805712e-07,
2.2743990730289e-07, 3.07180534936803e-07, 4.14878418164378e-07,
5.60335245682253e-07, 7.56789448222779e-07, 1.02212079550612e-06,
1.38047758295943e-06, 1.86447536195262e-06, 2.51816121915984e-06,
3.40041627253216e-06, 4.54641422109325e-06, 6.03834395349185e-06,
7.97982308417383e-06, 1.04817057864209e-05, 1.35489394526282e-05,
1.72865813618296e-05, 2.18309175451225e-05, 2.73477089217644e-05,
3.40380929265256e-05, 4.21460976943755e-05, 5.1967369819244e-05,
6.38600965206997e-05, 7.82579725998248e-05, 9.56860600237062e-05,
0.000116779922497502, 0.000142335963852117, 0.000173355233081032,
0.000210921169220437, 0.00025641423771755, 0.000311506843394084,
0.000378223660039666, 0.000459016772258694, 0.000556855446703318,
0.000675335852469291, 0.000818812559327979, 0.000992558463515475,
0.00120295979079978, 0.00145774933544351, 0.00176629223196222,
0.00213992675332361, 0.00259238540452746, 0.00314030080012767,
0.00380380663276417, 0.00460729241649197, 0.00558028623723877,
0.00675855195676351, 0.00818539089553454, 0.00991324940277193,
0.0120056289887936, 0.0145394320140841, 0.0176077795085524, 0.0213234607142798,
0.0258230276512022, 0.0312718588796218, 0.0378702107462816, 0.0458605985746323,
0.0555366906666179, 0.0672541473478419, 0.0814435879234418, 0.0986265500083953,
0.119434540978074, 0.144632361864515, 0.175146169178876, 0.212097172372404,
0.256843809691636, 0.310804466617569, 0.369842684226363, 0.431179045399307,
0.493945429064933, 0.557253598745863, 0.620207670785615, 0.681916748818428,
0.741507890725135, 0.7981374131588, 0.85100435722966, 0.899360296843544,
0.942521141956581, 0.979876115698495, 0.999812477868897, 0.972735811573507,
0.932054481163834, 0.885815978946983, 0.834672310063189, 0.779345135479752,
0.720614966194481, 0.659310357439126, 0.596295772938628, 0.532460446628508,
0.468704750726898, 0.405928059993783, 0.345016117261179, 0.286827900234236,
0.237623456225718, 0.19790417419609, 0.164452220923679, 0.136482929335078,
0.112955983834528, 0.0932654285994524, 0.0770066613579728, 0.0635815895825471,
0.0524963384973958, 0.0433430973402779, 0.0357851408660264, 0.0295444442412585,
0.0243914258497928, 0.0201365021470287, 0.0166231553258446, 0.0137221430720713,
0.0113267390267136, 0.00934882441245559, 0.00771563465768068,
0.00636709119593569, 0.00525358045912998, 0.00433414349100376,
0.00357495316102798, 0.00294808230359634, 0.00243046968641578,
0.00200307217108402, 0.00165016998349207, 0.00135877837976224,
0.00111817834219132, 0.000919518759694046, 0.000755491588934199,
0.000620062540625639, 0.000508249477581297, 0.000415939214900695,
0.000339735906332031, 0.000276836029518111, 0.000224925814050528,
0.000182095460069257, 0.000146769499059896, 0.000117648326182113,
9.36606547647744e-05, 7.39240003391358e-05, 5.77123463706654e-05,
4.44292627620613e-05, 3.35069132161542e-05, 2.30948965054054e-05,
1.35498521268301e-05, 6.6480335943903e-06, 3.22817353776792e-06,
1.56754636933548e-06, 7.6117394173847e-07, 3.69613102610182e-07,
1.79477797412926e-07, 8.71511930430619e-08, 4.23189904393637e-08,
2.05492170784783e-08, 9.97819224010812e-09, 4.84507812590914e-09,
2.3525233197402e-09, 1.1421808424864e-09, 5.54459053511967e-10,
2.69071150351853e-10, 1.30491713616467e-10, 6.32000285938001e-11,
3.05246463595271e-11, 1.46586964219514e-11, 6.95585084010912e-12,
3.218335275606e-12, 1.40934851021314e-12, 5.43057275709068e-13,
1.47366028903012e-13, 6.63775977550542e-15)), class = c("tbl_df",
"tbl", "data.frame"), row.names = c(NA, -205L))
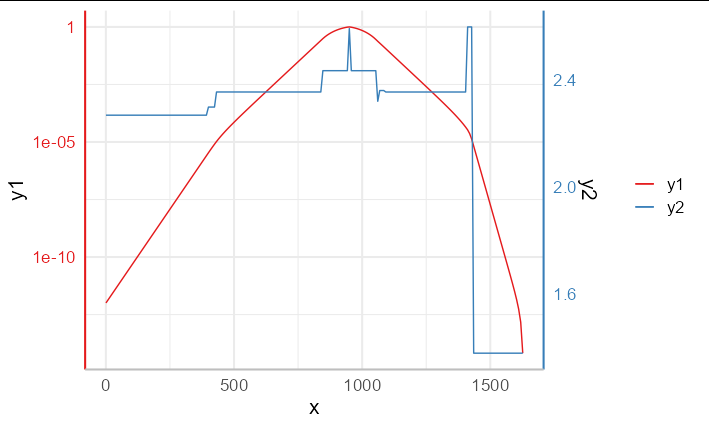
plot:
ylim.prim <- c(min(df$y1), max(df$y1))
ylim.sec <- c(min(df$y2), max(df$y2))
b <- diff(ylim.prim)/diff(ylim.sec)
a <- ylim.prim[1] - b*ylim.sec[1]
ggplot(df, aes(x=x))
geom_line(aes(y=y1, color = "y1"))
geom_line(aes(y = 10^(a y2*b), color = "y2"))
scale_y_log10(sec.axis = sec_axis(~ (log(., 10.0) - a)/b,
breaks = 1:6 * 0.5, name = "y2"))
coord_cartesian(
xlim = c(),
ylim=c(1e-10,3))
scale_color_brewer(palette = "Set1", name = NULL)
theme_minimal(base_size = 16)
theme(axis.line.y.left = element_line(color = "#E41A1C"),
axis.line.y.right = element_line(color = "#377EB8"),
axis.line.x.bottom = element_line("gray"),
axis.text.y.left = element_text(color = "#E41A1C"),
axis.text.y.right = element_text(color = "#377EB8"))
CodePudding user response:
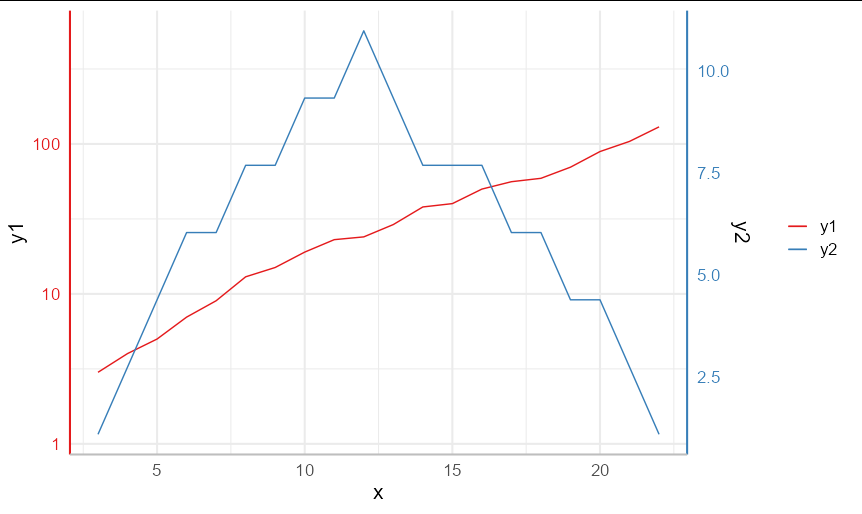
Showing which line belongs to which axis is simple enough by using colored theme elements and mapping each line to a color aesthetic.
The y1 series is approximately linear if we switch to scale_y_log10, which is also easy to do.
The difficult part is trying to get the second series mapped to a linear continuous axis when the primary axis is log scaled. To do this, we need to use the value of the second series as an exponent of some small number, chosen so that the scales of the two lines are approximately equal on your plot. We then need to take the log to the same base as part of our transformation in the secondary axis. In your case, 1.03 gives reasonable results:
ggplot(df, aes(x=x))
geom_line(aes(y=y1, color = "y1"))
geom_line(aes(y = 1.05^(a y2*b), color = "y2"))
scale_y_log10(sec.axis = sec_axis(~ (log(., 1.03) - a)/b,
breaks = 1:4 * 2.5, name = "y2"))
scale_color_brewer(palette = "Set1", name = NULL)
theme_minimal(base_size = 16)
theme(axis.line.y.left = element_line(color = "#E41A1C"),
axis.line.y.right = element_line(color = "#377EB8"),
axis.line.x.bottom = element_line("gray"),
axis.text.y.left = element_text(color = "#E41A1C"),
axis.text.y.right = element_text(color = "#377EB8"))
You can see that y1 is plotted on a log axis, but y2 is on a normal continuous axis.
As a caveat here, secondary axes are often frowned upon in data visualization, and having one axis on a log scale with the other being non-log is likely to make the plot very difficult for your audience to interpret.
Edit
A more general approach would be to log transform the series on the primary axis and transform its labels too. This allows using a continuous axis rather than log axis:
a <- range(log10(df$y1))
b <- range(df$y2)
ggplot(df, aes(x=x))
geom_line(aes(y=(log10(y1) - a[1])/diff(a), color = "y1"))
geom_line(aes(y = (y2 - b[1])/diff(b) , color = "y2"))
scale_y_continuous(
labels = ~ 10^(. * diff(a) a[1]),
breaks = (pretty(log10(df$y1)) - a[1])/diff(a), name = "y1",
sec.axis = sec_axis(~ diff(b) * . b[1], name = "y2"))
scale_color_brewer(palette = "Set1", name = NULL)
theme_minimal(base_size = 16)
theme(axis.line.y.left = element_line(color = "#E41A1C"),
axis.line.y.right = element_line(color = "#377EB8"),
axis.line.x.bottom = element_line("gray"),
axis.text.y.left = element_text(color = "#E41A1C"),
axis.text.y.right = element_text(color = "#377EB8"))