R finding list of coordinates in a hexagonal grid-CodePudding

Starting from the centre of this hexagonal grid and working outwards, I would like to generate a list of 100000 pairs of coordinates (without any coordinates duplicated). Looking for suggestions on the best way to do this. If possible I'd like them ordered from closest to the centre to furthest from the centre.

CodePudding user response：

The following function will find the centroids of hexagons in a regular grid, centered at x = 0, y = 0, where each hexagon is 1 unit wide:

hex_rings_at_d <- function(d) {

  if(d == 0) return(data.frame(x = 0, y = 0))
  d2 <- sqrt(d^2 - (0.5 * d)^2)
  d3 <- 0.5 * d
  f <- function(a, b) seq(a, b, length.out = d   1)[-1]
  
  data.frame(x = c(f( d,  d3), f( d3, -d3), f(-d3, -d), 
                   f(-d, -d3), f(-d3,  d3), f( d3,  d)),
             y = c(f(0, d2), f(d2, d2), f(d2, 0), 
                   f(0, -d2), f(-d2, -d2), f(-d2, 0)))
}

If we get all centroids out to a distance of 577 we will have 100,000 of them:

df <- do.call(rbind, lapply(0:577, hex_rings_at_d))

nrow(df)
#> [1] 1000519

These will be ordered from inside out:

head(df)
#>      x          y
#> 1  0.0  0.0000000
#> 2  0.5  0.8660254
#> 3 -0.5  0.8660254
#> 4 -1.0  0.0000000
#> 5 -0.5 -0.8660254
#> 6  0.5 -0.8660254

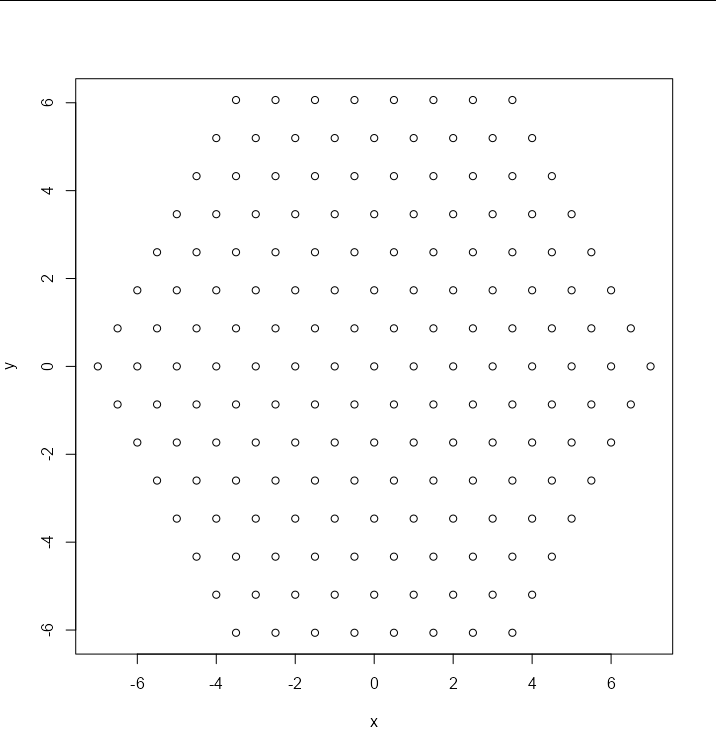
And we can confirm they are arranged in a regular hexagonal grid. Here are the first 169 centroids:

plot(df[1:169,])

^{Created on 2022-06-24 by the reprex package (v2.0.1)}