R count number of subgraphs/components in a graph-CodePudding

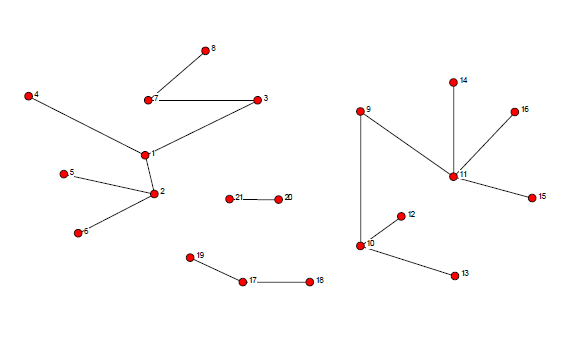
Does anyone know any R packages or methods to count the number of subgraph in a graph? I know igraph can handle some measurements of the graph, but I don't find related functions to count the number of subgraphs in a graph. For example, the number of subgraphs in the below graph should be 4.

Many thanks!

CodePudding user response：

You can use igraph::clusters.

library(igraph)
ig <- graph_from_data_frame(data)
plot(ig)


clusters(ig)
#$membership
#7  3  1  2 21 19 17 13 10  9 11  8  4  5  6 20 18 12 14 16 15 
#1  1  1  1  2  3  3  4  4  4  4  1  1  1  1  2  3  4  4  4  4 
#
#$csize
#[1] 8 2 3 8
#
#$no
#[1] 4

Element no returns the number of connected subgraphs (in this case 4). Element csize gives the number of connected nodes in every subgraph. Element membership is named vector returning the group number (the value) for every node (the name).

Sample data


data <- read.table(text = 
    "7   8
    7   3
    3   1
    1   4
    1   2
    2   5
    2   6
    21  20
    19  17
    17  18
    13  10
    10  12
    10  9
    9   11
    11  14
    11  16
    11  15", header = F)

CodePudding user response：

Most directly, you can use igraph::count_components:

count_components(ig)
# [1] 4

(Using Maurits's nicely shared sample data)

Component is a better term than subgraph for what you're looking for - a subgraph can be any subset of a graph, connected or not. Per wikipedia:

a component of an undirected graph is a connected subgraph that is not part of any larger connected subgraph. The components of any graph partition its vertices into disjoint sets, and are the induced subgraphs of those sets.

CodePudding user response：

I think count_components by Gregor Thomas is the most straightforward solution to your question.

Another option which is not that efficient is using decompose

> decompose(ig)
[[1]]
IGRAPH 5d09d0f DN-- 8 7 --
  attr: name (v/c)
  edges from 5d09d0f (vertex names):
[1] 7->3 7->8 3->1 1->2 1->4 2->5 2->6

[[2]]
IGRAPH 5d09d3e DN-- 2 1 --
  attr: name (v/c)
  edge from 5d09d3e (vertex names):
[1] 21->20

[[3]]
IGRAPH 5d09d64 DN-- 3 2 --
  attr: name (v/c)
  edges from 5d09d64 (vertex names):
[1] 19->17 17->18

[[4]]
IGRAPH 5d09d87 DN-- 8 7 --
  attr: name (v/c)
  edges from 5d09d87 (vertex names):
[1] 13->10 10->9  10->12 9 ->11 11->14 11->16 11->15

and you see the number of sub-graphs via length

> length(decompose(ig))
[1] 4