Sum of cubes in python-CodePudding

I would like to obtain a list of integers whose cubes add up to a target number. The integers in the list must all be distinct. My code works for all cases except for

n=sum([n*n*n for n in range(1001)])

...where the expected result is [6303, 457, 75, 14, 9, 7,5, 4] instead my output in my program is [6303, 457, 75, 15, 8, 4, 3, 2, 1]. How can I correct my program to correctly output the expected result?

def sum_of_cubes(n):
    original=n
    i=1
    lst=[]
    tot=0
    while i**3<=n:
        i =1
    lst.append(i-1)
    n-=(i-1)**3
    for j in range(lst[0],0,-1):
        if j**3<n:
            lst.append(j)
            n-=j**3
    if n==1:
        lst.append(n)
    for i in lst:
        tot =i**3
    #if original-tot>1:
        #return None
    return lst

n=sum([n*n*n for n in range(1001)])
print(sum_of_cubes(n))

CodePudding user response：

You can implement a backtracking search algorithm using a stack (instead of recursion). Of course, being an exponential algorithm, it only works for inputs of relatively small size.

from math import *

def sum_of_cubes(n):
    bag = []
    stack = [(floor(n**(1/3)), n, [])]                          # simulated initial call
    while stack:
        (k, n, s) = stack.pop()
        if n == 0: bag.append(s)
        elif k > 0:
            stack.append((k-1, n, s))                           # simulated recursive call
            if n-k**3 >= 0: stack.append((k-1, n-k**3, [k] s))  # simulated recursive call
    return bag

Examples:

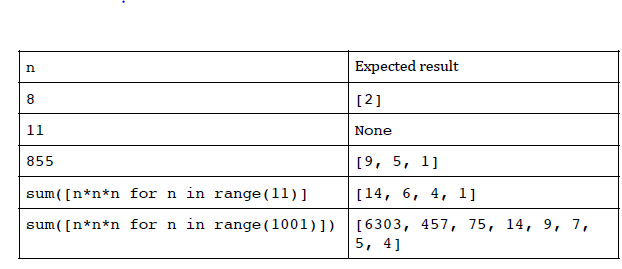
>>> sum_of_cubes(8)
[[2]]

>>> sum_of_cubes(11)
[]

>>> sum_of_cubes(855)
[[1, 5, 9], [7, 8]]

>>> sum_of_cubes(3473)
[[9, 14], [1, 6, 8, 14], [1, 3, 4, 5, 8, 14], [2, 3, 8, 9, 13], [1, 2, 4, 5, 6, 11, 12], [1, 2, 3, 5, 7, 8, 9, 12], [2, 4, 5, 6, 9, 10, 11]]

>>> sum_of_cubes(sum(n**3 for n in range(11)))
[[1, 4, 6, 14], [2, 3, 4, 9, 13], [1, 2, 3, 4, 6, 8, 13], [1, 2, 6, 7, 9, 12], [1, 2, 3, 4, 5, 7, 9, 12], [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]]

>>> sum_of_cubes(15000)
[[2, 3, 5, 6, 9, 12, 23], [3, 5, 8, 10, 11, 14, 21], [3, 9, 11, 17, 20], [1, 3, 6, 8, 11, 17, 20], [2, 4, 5, 6, 7, 11, 17, 20], [2, 3, 5, 14, 16, 20], [3, 5, 9, 14, 15, 20], [1, 3, 5, 6, 8, 14, 15, 20], [6, 8, 11, 13, 14, 20], [3, 4, 5, 8, 11, 13, 14, 20], [2, 4, 5, 10, 11, 12, 14, 20], [5, 7, 9, 11, 12, 14, 20], [1, 5, 6, 7, 8, 11, 12, 14, 20], [5, 6, 7, 8, 9, 10, 11, 14, 20], [2, 3, 5, 7, 8, 9, 11, 12, 13, 20], [3, 5, 6, 8, 15, 17, 18], [5, 6, 7, 8, 11, 12, 17, 18], [1, 2, 5, 7, 8, 9, 11, 14, 15, 18], [2, 3, 5, 6, 8, 12, 15, 16, 17], [2, 3, 4, 5, 6, 11, 13, 14, 15, 17]]

Remark If you are interested in getting only one of the possible solutions, you can use this other version of the algorithm:

def sum_of_cubes(n):
    stack = [(floor(n**(1/3)), n, [])]
    while stack:
        (k, n, s) = stack.pop()
        if n == 0: return s
        elif k > 0:
            stack.append((k-1, n, s))
            if n-k**3 >= 0: stack.append((k-1, n-k**3, [k] s))

Example:

>>> sum_of_cubes(sum(n**3 for n in range(1001)))
[4, 5, 7, 9, 14, 75, 457, 6303]

CodePudding user response：

The problem with your algorithm is this:

    while i**3 <= n:
        i  = 1
    lst.append(i-1)

It appends "15" which is lesser than "14" "9", so your algorytm would not also work for n=3473 for example, wich is 14^3 9^3.

Solution: The only thing I can think of it is maybe to make the forbidden list, basically your algorithm first tries the original one, if it fails, try variants that exclude 1-all member/s of that unsuccessful list...or something like that maybe?

Also you should have checker like:

if original != tot:
  doSomething()
  lst=[]
  etc....

This should get you to right track, good luck.

EDIT:

Ok so recursive function would solve the problem...if you had infinite CPU power/time, i will show solution to eliminate ONE black member, if there would be 2 or more numbers like 15, it will fail.


if original != tot:
  lst= doSomething(original, lst)

doSomething(n,lst):
    returnList=[]
    newList=[]
    orig=n
    for blackMember in lst:
        n=orig
        #basicaly what you wrote before but try add before append and lowering n
        if theNumberYOuWantToAdd != blackMember:
            n -= theNumberYOuWantToAdd**3
            newList.append(theNumberYOuWantToAdd)
    
    ....
    ....
    ....
    if tot == original:
        returnList = newList
    #ofc if you want recursive functions you can do this just...it will freeze on big numbers: 
    #else:
        #superBlastlist = newList   lst #dunno how to connect them, but you have idea
        #returnList=doSomething(orig, superBlastlist)
    return returnList

So you have idea... So basically, for 1-2 levels of blacklisting numbers, it would be CPU acceptable, but i would reccomend dont go above 1e10 combinations, then even GPU helping would not save you :D