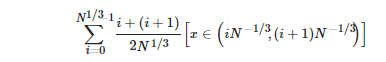How fix a problem when I change the expression of `x_new` inside the following function `phix`?-CodePudding

The code for this function is as follows.

def phix(x, N):
  lam=np.floor(N**(1/3))
  x_new=0
  for i in range(0, int(lam)):
   if (i 1)*N**(-1/3)>x>i*N**(-1/3):
    x_new=x_new (2*i 1)/(2*N**(1/3))
  return x_new

N=1000
x=0.57
phix(x, N)

0.55

If I replace x_new by phix(x,N) directly, there will be a problem, because the function I define here can only work on one x, not N many x. How to fix it?

def adapW1_eot(x,y,N):
    x_new = phix(x,N)
    y_new =  N**(-1/3)*np.floor(N**(1/3)*y)

    x_val = np.array(list(Counter(x_new).keys()))
    x_freq = np.array(list(Counter(x_new).values()))
    W = np.zeros(len(x_val))
    for i in range(0,len(x_val)):
        aux = y_new[x_new==x_val[i]]
        aux = aux.reshape((len(aux), 1))
        c = np.abs(aux-y_new)
        w1 = np.ones(len(aux))/len(aux)
        w2 = np.ones(len(y))/len(y)
        W[i] = ot.sinkhorn2(w1,w2,c,0.01)
    c = np.abs(y_new.reshape((N,1))-y_new)
    denom = c.sum()/N**2
    return np.dot(W, x_freq)/(N*denom)

N=5
x = np.random.random_sample(N)
y = np.random.random_sample(N)
adapW1_eot(x,y,N)

ValueError: The truth value of an array with more than one element is ambiguous. Use a.any() or a.all()

CodePudding user response：

Assuming that N is always a constant, you can use numpy.vectorize:

def adapW1_eot(x, y, N: int):
    x_new = np.vectorize(phix)(x, N)
    ...

Then x_new will be a NumPy array.

CodePudding user response：

Even though, you could just use np.vectorize, you may better step back and re-think what actually happens when working with numpy arrays. This will help you to write more efficient/faster code, so you do not start blaming python for being slow :-).

In the original function, you want to replace the following line

x_new = N**(-1/3)*np.floor(N**(1/3)*x)

where N is an integer and x is an array of floats. Assuming that x is one dimensional, this is equivalent to

# allocate memory for new array
x_new = np.empty_like(x)
# calculate the spacing
step = N**(-1/3)
# loop though elements in x
for i in range(len(x)):
    # access x at position i
    x_i = x[i]
    # use floor division to get the bin index
    bin_idx = x_i // step
    # set the new value at position i in x_new
    x_new[i] = bin_idx * step

Such a loop in python would be very slow, so numpy implements a shortcut which looks like working with a single position. Let us now split the one liner a bit, to separate the steps still using fast numpy loops under the hood.

step = N**(-1/3)
bin_idx = x // step
x_new = step * bin_idx

What you want are the middle points of those bins, which you can easily calculate now

step = N**(-1/3)
bin_idx = x // step
x_new = step * (2*bin_idx   1)/2

You see, that there was no need to introduce a function which loops on the bin spacing when understanding the original idea which uses the floor division to bin the data.

The following is beyond the question, but still worth to point out. The next lines in your code could also improve a bit

x_val = np.array(list(Counter(x_new).keys()))
x_freq = np.array(list(Counter(x_new).values()))

What the counter does is basically summing how many values fall into the bin. Even though it is not extremely expensive, you should not do that twice, but instead re-use the instance counter = Counter(x_new). However, what you are doing here is building a histogram. Since you already computed the bin values x_new, you can use x_val, x_freq = np.unique(x_new, return_counts=True) to get the frequencies.

Please note that the way you want to re-label x_new will not change the result of your function. So there is not really a benefit in doing it unless you implement a non-equal spacing for the bins.