In R, the output of my linear model shows a positive correlation but my ggplot graph indicates a neg-CodePudding

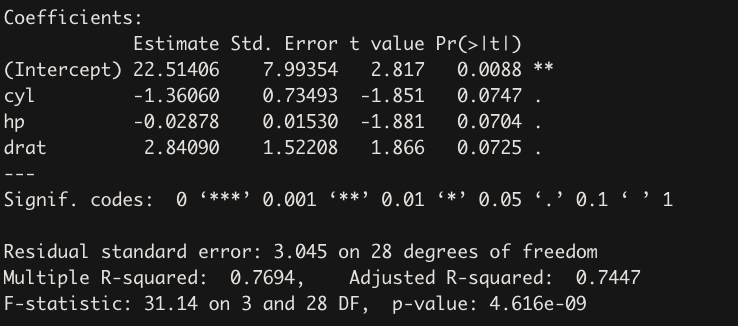
I'm trying to identify the impact of how Sycamore_biomass affects the day which a bird lays its first_egg. My model output indicates a weak positive relationship - i.e. as sycamore biomass increases, the day of the first egg being laid should increase (i.e. should be later) (note I'm including confounding factors in this model):

Call:
lm(formula = First_egg ~ Sycamore_biomass   Distance_to_road   
    Distance_to_light   Anthropogenic_cover   Canopy_cover, data = egglay_date)

Coefficients:
                    Estimate Std. Error t value Pr(>|t|)  
(Intercept)         39.61055   16.21391   2.443   0.0347 *
Sycamore_biomass     0.15123    0.53977   0.280   0.7851  
Distance_to_road     0.01773    0.46323   0.038   0.9702  
Distance_to_light   -0.02626    0.44225  -0.059   0.9538  
Anthropogenic_cover -0.13879    0.28306  -0.490   0.6345  
Canopy_cover        -0.30219    0.20057  -1.507   0.1628  
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 12.99 on 10 degrees of freedom
Multiple R-squared:  0.2363,    Adjusted R-squared:  -0.1455 
F-statistic: 0.6189 on 5 and 10 DF,  p-value: 0.6891

However, when I plot this using ggplot, the regression line indicates a negative relationship? Can anyone help me out with what is happening here?

ggplot(egglay_date, aes(x=Sycamore_biomass, y=First_egg))  
  geom_point(shape=19, alpha=1/4)  
  geom_smooth(method=lm)

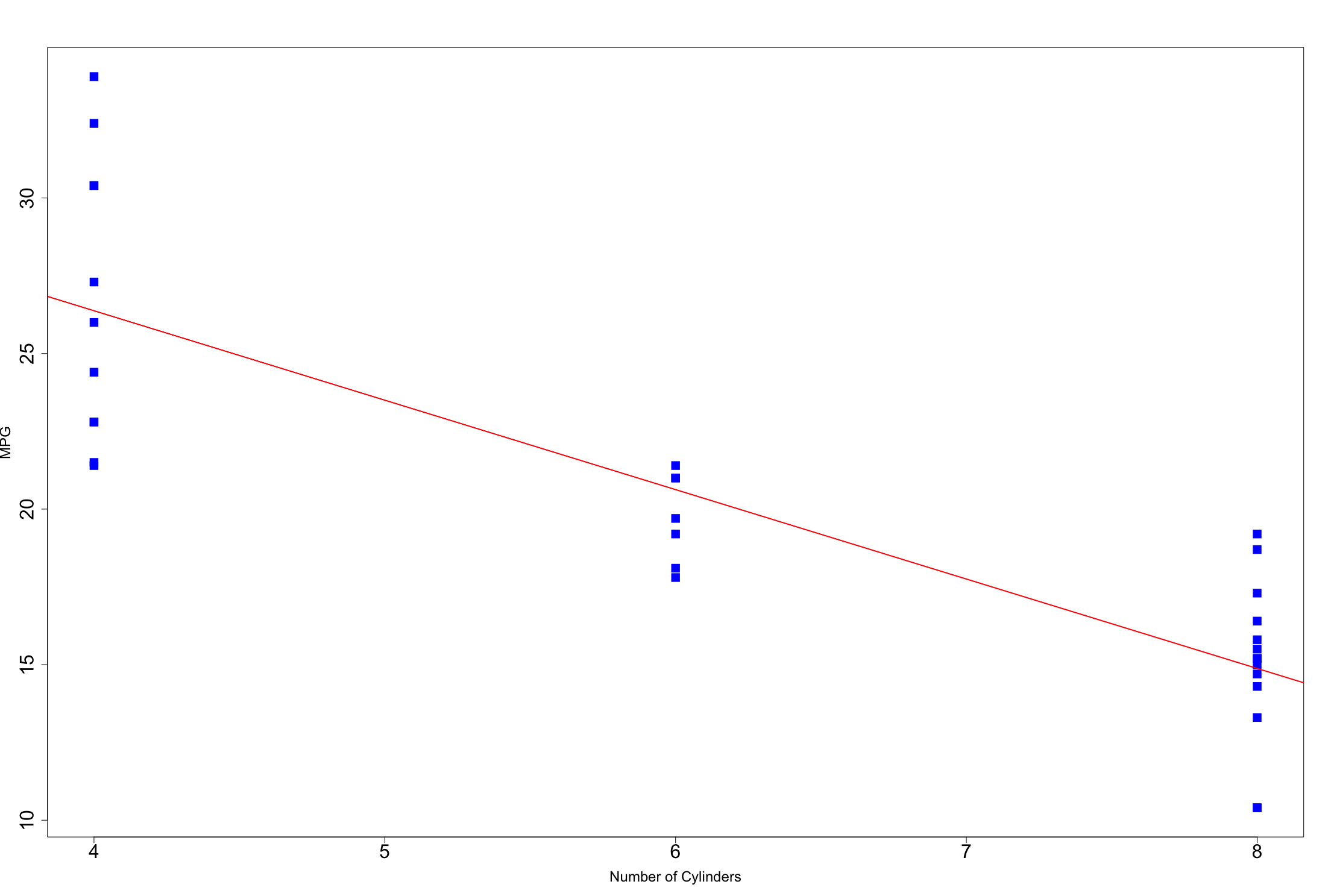
So I do what you just did and just plot mpg~cly (without considering my other variables)

plot(mpg~cyl, pch=15, col="blue",cex=2, cex.axis=2, ylab="MPG", xlab="Number of Cylinders", cex.lab=1.5)
abline(lm(mpg~cyl),lwd=2,col="red")

First off, we see that the y intercept is not 22.5, but rather above 25.

If I were to do the math from first model, if I had 4 cylinders, I should predict:

22.51406 (4 * -1.3606) = 17.07

So lets see if our prediction is correct on our graph

Definitely not.

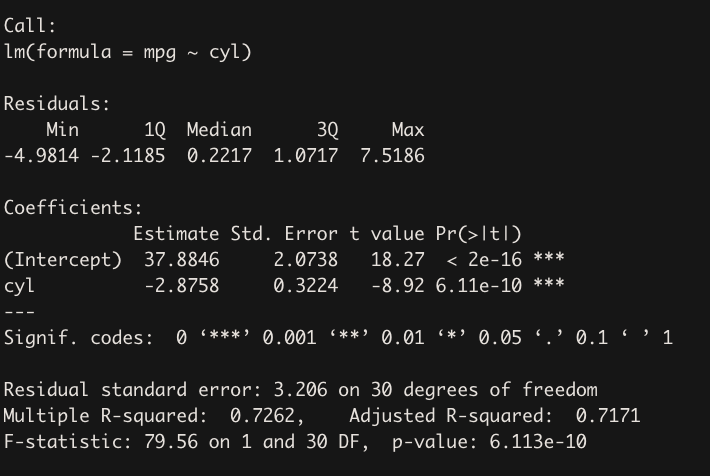
So lets run a new model (which you need to do), where we model just mpg~cly

reduced_model <- lm(mpg~cyl)

summary(reduced_model)

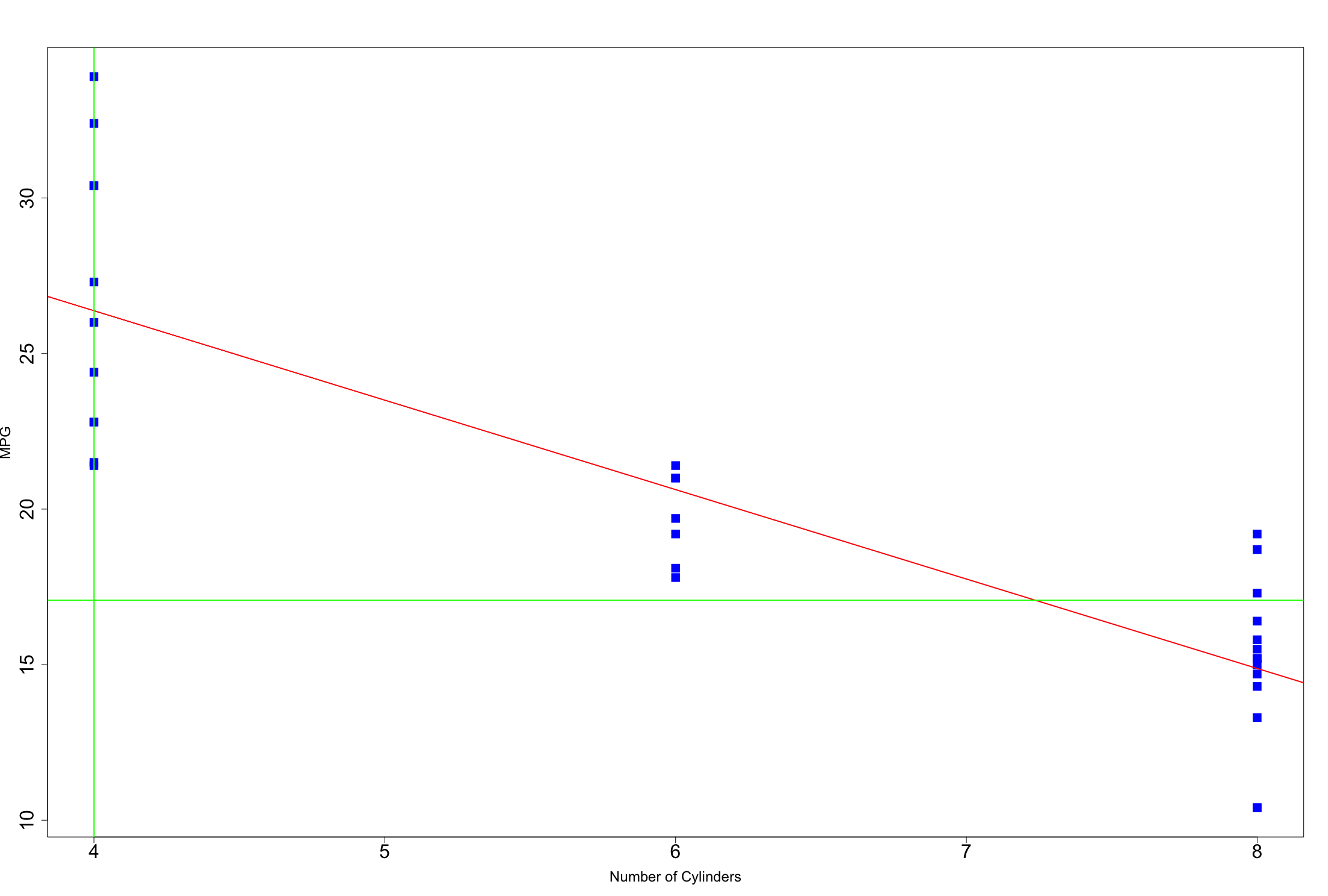
See how the intercept and coefficent (estimates) changed? Yours will too when you run a reduced model. Lets see if the plots now make sense following the same steps as above with predicting 4 cylinders

37.8846    (4 * -2.8758 ) # 26.38
plot(mpg~cyl, pch=15, col="blue",cex=2, cex.axis=2, ylab="MPG", xlab="Number of Cylinders", cex.lab=1.5)
abline(lm(mpg~cyl),lwd=2,col="red")
abline(h=26.38,v=4,lwd=2, col="green")

Looks like everything checks out.

Summary: You need to run a simple model with just your two variables of interest if you want to correctly understand your plot