I am calculating points along a three-dimensional logarithmic spiral between two points. I seem to be close, but I think I'm missing a conditional sign flip somewhere.
This code works relatively well:
using PlotlyJS
using LinearAlgebra
# Points to connect (`p2` spirals into `p1`)
p1 = [1,1,1]
p2 = [3,10,2]
# Number of curve revolutions
rev = 3
# Number of points defining the curve
rez = 500 # Number of points defining the line
r = norm(p1-p2)
t = range(0,r,rez)
theta_offset = atan((p1[2]-p2[2])/(p1[1]-p2[1]))
theta = range(0, 2*pi*rev, rez) . theta_offset
x = cos.(theta).*exp.(-t).*r. p1[1];
y = sin.(theta).*exp.(-t).*r. p1[2];
z = exp.(-t).*log.(r). p1[3]
# Plot curve points
plot(scatter(x=x, y=y, z=z, marker=attr(size=2,color="red"),type="scatter3d"))
and produces the following plot. Values of the endpoints are shown on the plot, with an arrow from the coordinate to its respective marker. The first point is off, but it's close enough for my liking.
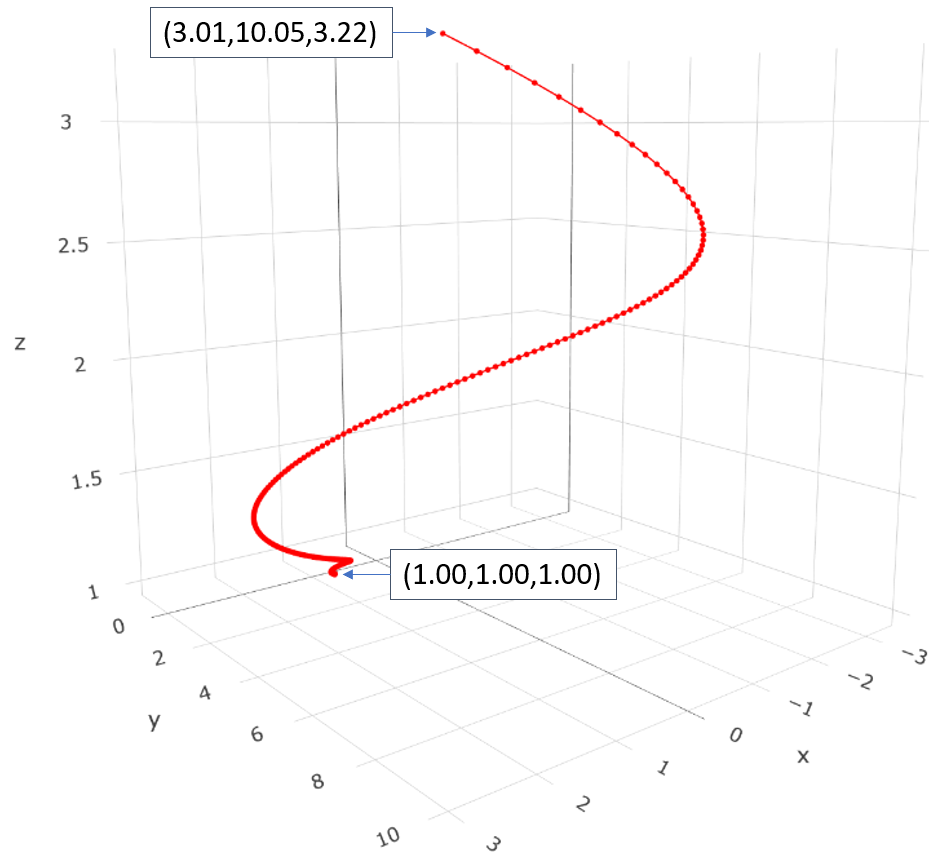
The problem comes when I flip p2 and p1 such that
p1 = [3,10,2]
p2 = [1,1,1]
In this case, I still get a spiral from p2 to p1, and the end point (p1) is highly accurate. However, the other endpoint (p2) is wildly off:
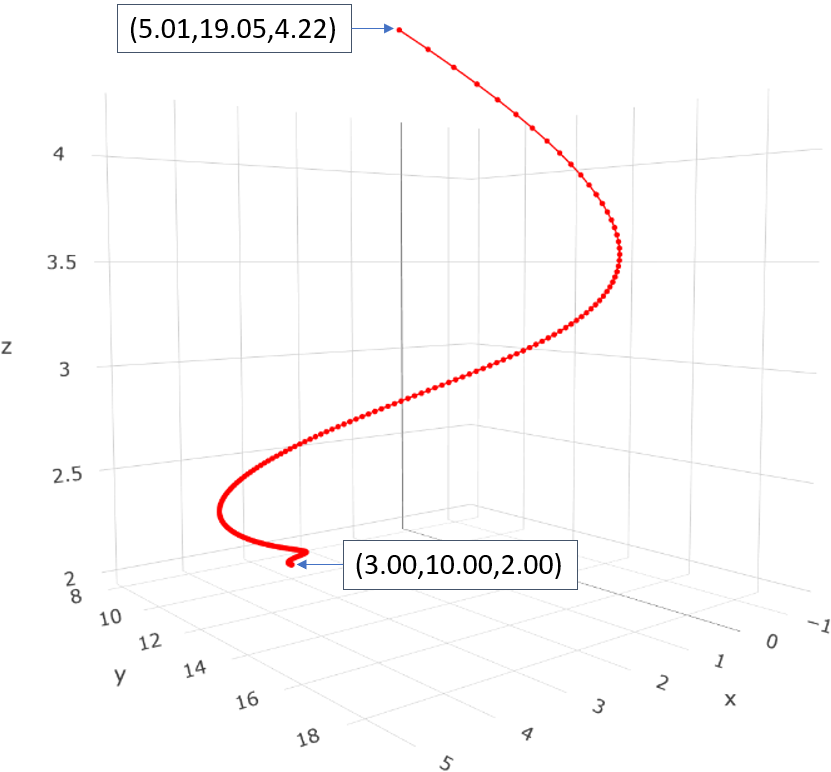
I think this is due to me changing the relative Z position of the two points, but I'm not sure, and I haven't been able to solve this riddle. Any help would be greatly appreciated. (Bonus points if you can help figure out why the Z value on p2 is off in the first example!)
CodePudding user response:
Assuming this is a follow-up of your other question: Drawing an equiangular spiral between two known points in Julia
I assume you just want to add a third dimension to your previous 2D problem using cylindric coordinate system. This means that you need to separate the treatment of x and y coordinate on one side, and the z coordinate on the other side.
First you need to calculate your r on the first two coordinate:
r = norm(p1[1:2]-p2[1:2])
Then, when calculating z, you need to take only the third dimension in your formula (not sure why you used a log function there in the first place):
z = exp.(-t).*(p1[3]-p2[3]). p2[3]
That will fix your z-axis.
Finally for your x and y coordinate, use the two argument atan function:
julia>?atan
help?> atan
atan(y)
atan(y, x)
Compute the inverse tangent of y or y/x, respectively.
For one argument, this is the angle in radians between the positive x-axis and the point (1, y), returning a value in the interval [-\pi/2, \pi/2].
For two arguments, this is the angle in radians between the positive x-axis and the point (x, y), returning a value in the interval [-\pi, \pi]. This corresponds to a standard atan2
(https://en.wikipedia.org/wiki/Atan2) function. Note that by convention atan(0.0,x) is defined as \pi and atan(-0.0,x) is defined as -\pi when x < 0.
like this:
theta_offset = atan( p1[2]-p2[2], p1[1]-p2[1] )
And finally, like in your previous question, add the p2 point instead of the p1 point at the end of x, y, and z:
x = cos.(theta).*exp.(-t).*r. p2[1];
y = sin.(theta).*exp.(-t).*r. p2[2];
z = exp.(-t).*(p1[3]-p2[3]). p2[3]
In the end, I have this:
using PlotlyJS
using LinearAlgebra
# Points to connect (`p2` spirals into `p1`)
p2 = [1,1,1]
p1 = [3,10,2]
# Number of curve revolutions
rev = 3
# Number of points defining the curve
rez = 500 # Number of points defining the line
r = norm(p1[1:2]-p2[1:2])
t = range(0.,norm(p1-p2), length=rez)
theta_offset = atan( p1[2]-p2[2], p1[1]-p2[1] )
theta = range(0., 2*pi*rev, length=rez) . theta_offset
x = cos.(theta).*exp.(-t).*r. p2[1];
y = sin.(theta).*exp.(-t).*r. p2[2];
z = exp.(-t).*(p1[3]-p2[3]). p2[3]
@show (x[begin], y[begin], z[begin])
@show (x[end], y[end], z[end]);
# Plot curve points
plot(scatter(x=x, y=y, z=z, marker=attr(size=2,color="red"),type="scatter3d"))
Which give the expected results:
p2 = [1,1,1]
p1 = [3,10,2]
(x[begin], y[begin], z[begin]) = (3.0, 10.0, 2.0)
(x[end], y[end], z[end]) = (1.0001877364735474, 1.0008448141309634, 1.0000938682367737)
and:
p1 = [1,1,1]
p2 = [3,10,2]
(x[begin], y[begin], z[begin]) = (0.9999999999999987, 1.0, 1.0)
(x[end], y[end], z[end]) = (2.9998122635264526, 9.999155185869036, 1.9999061317632263)
CodePudding user response:
In 2D, let us assume the pole at the point C, and the spiral from P to Q, corresponding to a variation of the parameter in the interval [0, 1].
We have
X = Cx cos(at b).e^(ct d)
Y = Cy sin(at b).e^(ct d)
Using the known points,
Px - Cx = cos(b).e^d
Py - Cy = sin(b).e^d
Qx - Cx = cos(a b).e^(c d)
Qy - Cy = sin(a b).e^(c d)
From the first two, by a Cartesian to polar transformation (and logarithm), you can obtain b and d. From the last two, you similarly obtain a b and c d, and the spiral is now defined.
For the Z coordinate, I cannot answer precisely as you don't describe how you generalize the spiral to 3D. Anyway, we can assume a certain function Z(t), that you can map to [Pz, Qz] by the linear transformation
(Qz - Pz) . (Z(t) - Z(0)) / (Z(1) - Z(0)) Pz.
