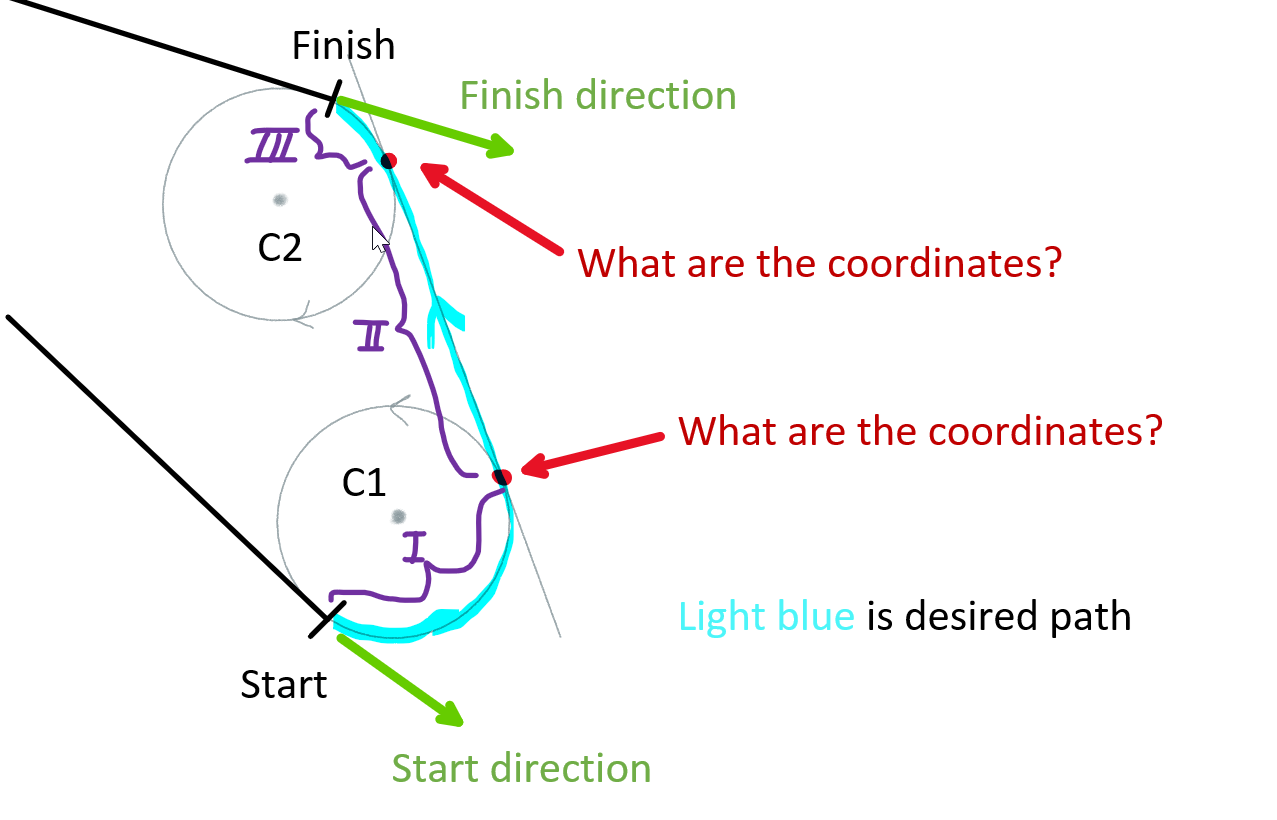
I'm trying to calculate a path from Start point (T-like black shape) with Start direction (green) to Finish point with finish direction in 2D space. The whole path (light blue) is a bunch of points. I need to find positions of two red points. The problem is that in most cases circle sections (I and III purple) has not equal amount of points i.e. different length. Start and finish directions can be any from 0 to 359 degrees.

CodePudding user response：

To make this a programming question, here is an implementation for getting the two tangent points (the red points).

This implementation defines Vector and Circle classes, each with methods to create new results from them. The Circle class has a tangentWith method, which takes another circle as argument and returns an array with two Vectors, i.e. the coordinates of the two red points.

The snippet below is interactive. It starts with the initial two circles, as depicted in your question, but allows you to draw alternative circles using the mouse (click to determine center of circle, and drag to set its radius):

class Vector {
    constructor(x, y) {
        this.x = x;
        this.y = y;
        // Derive polar coordinates:
        this.size = (x ** 2   y ** 2) ** 0.5;
        this.angle = Math.atan2(this.y, this.x);
    }
    subtract(v) {
        return new Vector(this.x - v.x, this.y - v.y);
    }
    add(v) {
        return new Vector(this.x   v.x, this.y   v.y);
    }
    multiplyBy(scalar) {
        return new Vector(this.x * scalar, this.y * scalar);
    }
    resize(size) {
        return this.multiplyBy(size / this.size);
    }
    rotate(angle) {
        angle  = this.angle;
        return new Vector(this.size * Math.cos(angle), this.size * Math.sin(angle));
    }
}

class Circle extends Vector {
    constructor(x=0, y=0, radius=0) {
        super(x, y);
        this.radius = radius;
    }
    touch(v) { // Set radius so that v is on the circle
        return Circle.fromVector(this, this.subtract(v).size);
    }
    tangentWith(other) { // Main algorithm
        let v = this.subtract(other);
        const sinus = (this.radius - other.radius) / v.size;
        if (Math.abs(sinus) > 1) return []; // One circle includes the other: no tangent
        v = v.rotate(Math.asin(sinus)   Math.PI / 2);
        return [v.resize(this.radius).add(this), v.resize(other.radius).add(other)];
    }
    static fromVector(v, radius=0) {
        return new Circle(v.x, v.y, radius);
    }
}

// The circles as depicted in the question
const circles = [new Circle(50, 50, 25), new Circle(80, 120, 25)];

// I/O management, allowing to draw different circles
const canvas = document.querySelector("canvas");
const ctx = canvas.getContext("2d");

function mouseVector(e) {
    return new Vector(e.clientX - canvas.offsetLeft, e.clientY - canvas.offsetTop);
}

canvas.addEventListener("mousedown", e => {
    circles.reverse()[0] = Circle.fromVector(mouseVector(e));
});

canvas.addEventListener("mousemove", e => {
    if (!e.buttons) return;
    circles[0] = circles[0].touch(mouseVector(e));
    draw();
});

function drawCircle(c) {
    ctx.beginPath();
    ctx.arc(c.x, c.y, c.radius, 0, 2*Math.PI);
    ctx.stroke();
}

function drawSegment(start, end) {
    if (!start) return;
    ctx.beginPath();
    ctx.moveTo(start.x, start.y);
    ctx.lineTo(end.x, end.y);
    ctx.stroke();
}

function draw() {
    ctx.clearRect(0, 0, canvas.width, canvas.height);
    circles.map(drawCircle);
    drawSegment(...circles[0].tangentWith(circles[1]));
}
draw();

canvas { border: 1px solid }

First draw C1, then C2 (use mouse drag)<br>
<canvas width="600" height="150"></canvas>

CodePudding user response：

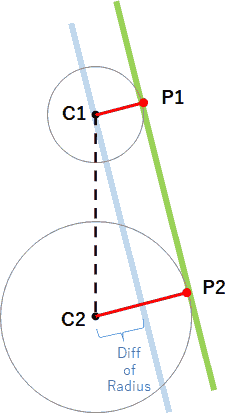
I drawn a simple figure:

As you see, red line directional component of the vector (C1 - C2) or (C2 - C1) equals difference of radius.
(Roughly) writing this relation as a equation,

• Inner-Product( C1 -C2, U ) = dr
• dr = | r1 - r2 |

where U is unit vector has direction along the red line, and 2 scalars {r1, r2} are circle radius.
This becomes to:

| C1 - C2 | * | U | * cos(theta) = | C1 - C2 | * 1 * cos(theta) = dr

where theta is the angle between (C1-C2) and U. Now you can calculate the cos(theta) value as:

cos(theta) = dr / | C1-C2 |