How to plot a function with different colour in Mathematica?-CodePudding

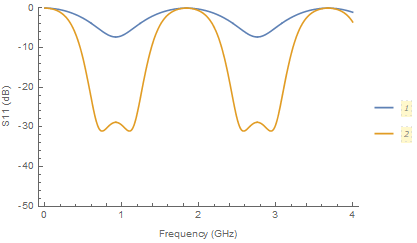
I tried to plot the function of S11 with different values of Z0e and my code is shown in the following.

Z0e = {120, 240}; Z0o = 60; ZS = 50; ZL = 100;

theta = (Pi/2)*(f/0.92);

Z11 = -I*(Z0e   Z0o)*Cot[theta]/2;
Z22 = -I*(Z0e   Z0o)*Cot[theta]/2;
Z12 = -I*(Z0e - Z0o)*Csc[theta]/2;
Z21 = -I*(Z0e - Z0o)*Csc[theta]/2;
ABCDpcl = ({
    {Z11/Z21, (Z11*Z22 - Z12*Z21)/Z21},
    {1/Z21, Z22/Z21}
   });
Apcl = ABCDpcl[[1, 1]];
Bpcl = ABCDpcl[[1, 2]];
Cpcl = ABCDpcl[[2, 1]];
Dpcl = ABCDpcl[[2, 2]];

S11pcl = (Apcl*ZL   Bpcl - Cpcl*ZS*ZL - Dpcl*ZS)/(Apcl*ZL   Bpcl   
     Cpcl*ZS*ZL   Dpcl*ZS);

Plot[20*Log[Abs[S11pcl]], {f, 0, 4}, PlotRange -> {-50, 0}, 
 Frame -> {{True, False}, {True, False}}, 
 FrameLabel -> {{"S11 (dB)", None}, {"Frequency (GHz)", None}}]

Below is my result.

Less elegant alternatives: evaluating the function twice

Plot[{First[20*Log[Abs[S11pcl]]], Last[20*Log[Abs[S11pcl]]]}, {f, 0, 4},
 PlotRange -> {-50, 0}, Frame -> {{True, False}, {True, False}}, 
 FrameLabel -> {{"S11 (dB)", None}, {"Frequency (GHz)", None}},
 PlotLegends -> Automatic]

or using Table and ListPlot

out = Table[Prepend[20*Log[Abs[S11pcl]], f], {f, 0.01, 4, 0.01}];
ListLinePlot[{out[[All, {1, 2}]], out[[All, {1, 3}]]}, 
 PlotRange -> {-50, 0}, Frame -> {{True, False}, {True, False}}, 
 FrameLabel -> {{"S11 (dB)", None}, {"Frequency (GHz)", None}},
 PlotLegends -> Automatic]