Is there a R function to derive a "kink"-CodePudding

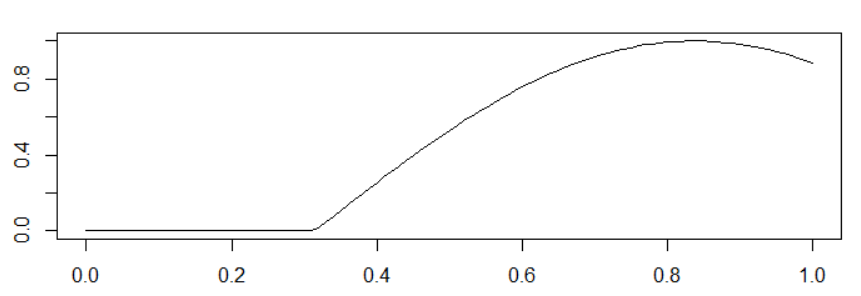
Suppose I have a function with a kink. I want to derive a kink point, which in this case is 0.314. I tried optim but it does not work.

Here is an example. In general, I want to derive c. Of course, I could use brute force, but it is slow.

# function with a kink
f <- function(x, c){
  (x >= 0 & x < c) * 0   (x >= c & x <=1) * (sin(3*(x-c)))   
    (x < 0 | x > 1) * 100
}

# plot
x_vec <- seq(0, 1, .01)
plot(x_vec, f(x_vec, c = pi/10), "l")

# does not work
optim(.4, f, c = pi/10)

CodePudding user response：

This function has no unique minimum.

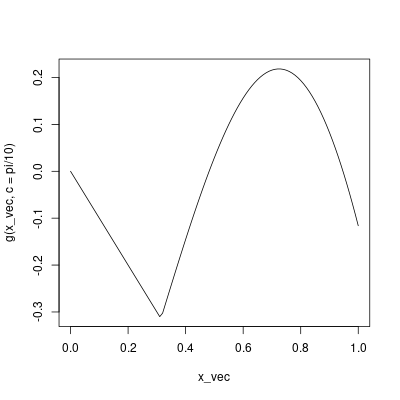
Here, a trick is to transform this function a little bit, so that its kink becomes a unique minimum.

g <- function (x, c) f(x, c) - x

x_vec <- seq(0, 1, 0.01)
plot(x_vec, g(x_vec, c = pi/10), type = "l")

# now works
optim(0.4, g, c = pi/10, method = "BFGS")
#$par
#[1] 0.3140978
#
#$value
#[1] -0.3140978
#
#$counts
#function gradient 
#      34        5 
#
#$convergence
#[1] 0
#
#$message
#NULL

Note:

In mathematics, if we want to find something, we have to first define it precisely. So what is a "kink" exactly? In this example, you refer to the parameter c = pi / 10. But what is it in general? Without a clear definition, there is no algorithm/function to get it.