How to modulate the size of the nodes of a network analysis with a certain value for each edge?-CodePudding

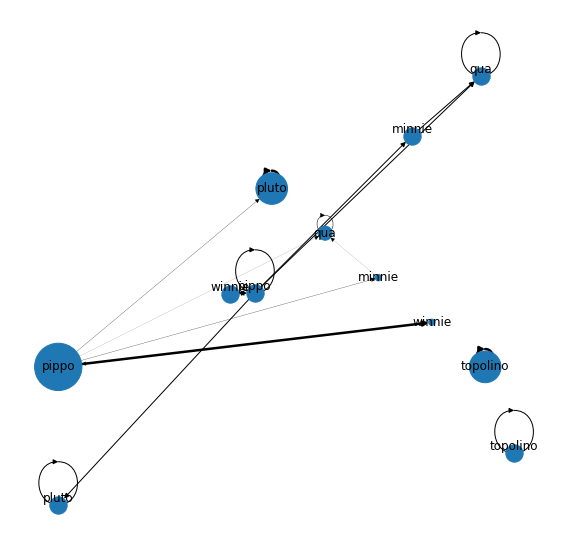
in the current graph the size of the nodes is given by the "count" of the arcs (e.g. node a going to a and b will be larger than the other two nodes that have no arcs to other nodes). the excel file is composed as follows:

column 0 (date[0]) = value of the oriented arc
column 1 (data[1]) = node a (node from where the oriented arc starts)
column 2 (data[2]) = node b (node from where the directed arc arrives)

Code:

import networkx as nx
import matplotlib.pyplot as plt
import xlrd

file = '/a/example.xlsx'

G= nx.DiGraph()
nations = []

book = xlrd.open_workbook(file)
sheet=book.sheet_by_index(0)

for row in range(sheet.nrows):
    data= sheet.row_slice(row)
    Orig = data[1].value
    Bene = data[2].value
    nations.append((Orig, Bene))
    
pos = nx.planar_layout(G)
betCent = nx.betweenness_centrality(G, normalized=True, endpoints=True)
node_colors = [20000.0*G.degree(v) for v in G]
node_sizes =  [v*7000 for v in betCent.values()]
 
plt.figure(figsize=(25,20))
nx.draw_networkx(G, pos=pos, with_labels=True,
                 node_color = node_colors,
                 node_size = node_sizes)
plt.axis('off')
G.add_edges_from(nations)
nx.draw(G,with_labels= True, verticalalignment='bottom')
plt.show()

Here the sample dataset:

df = pd.DataFrame({
    'weight':['50'] * 4   ['500'] * 5   ['20'] * 3   ['100'],
    'node a':['pippo', 'pippo', 'pippo', 'pluto', 'pippo', 'pippo',
             'pluto', 'topolino', 'qua', 'minnie', 'winnie', 'pippo', 'qua'],
    'node b':['pluto', 'qua', 'minnie', 'pluto', 'winnie', 'pippo',
             'pluto', 'topolino', 'qua', 'qua', 'pippo', 'qua', 'qua'],
    })

CodePudding user response：

Below I show, how to calculate the sum of edge weights of outgoing edges and scale the nodes accordingly:

import networkx as nx
import matplotlib.pyplot as plt
import pandas as pd

df = pd.DataFrame({
    'weight':['50'] * 4   ['500'] * 5   ['20'] * 3   ['100'],
    'node a':['pippo', 'pippo', 'pippo', 'pluto', 'pippo', 'pippo',
             'pluto', 'topolino', 'qua', 'minnie', 'winnie', 'pippo', 'qua'],
    'node b':['pluto', 'qua', 'minnie', 'pluto', 'winnie', 'pippo',
             'pluto', 'topolino', 'qua', 'qua', 'pippo', 'qua', 'qua'],
    })


G= nx.DiGraph()
nations = []

for index, row in df.iterrows():
    Orig = row[1]
    Bene = row[2]
    weight = float(row[0]) 
    #add the wight of each edge as an attribute 
    nations.append((Orig, Bene, {'weight':weight}))

#generate Graph
G.add_edges_from(nations)

#iterate over nodes and sum the weight of their outgoing edges, save on graph as node attribute
nodes_weight = {}
for n in G.nodes():
    nodes_weight[n]={'node_weight':sum([d['weight'] for o,b,d in G.out_edges(n, data=True)])}
    
nx.set_node_attributes(G, nodes_weight)  

#draw graph
pos = nx.planar_layout(G)

#calculate node size from attribute
node_sizes =  [v*2 for v in list(nx.get_node_attributes(G, 'node_weight').values())]

#similar if you want to change edge sizes
edge_sizes = [v/200 for v in list(nx.get_edge_attributes(G, 'weight').values())]

plt.figure(figsize=(10,10))

nx.draw_networkx(G, pos=pos, with_labels=True,
                 width = edge_sizes,
                 node_size = node_sizes)
plt.axis('off')

nx.draw(G,with_labels= True, verticalalignment='bottom')
plt.show()

Output: