Given a DAG and multiple sources S1 .. Sn, we define a valid node as a node that is reachable from all sources. Find out all the valid nodes which don't have a valid parent.

Effectively, find the direct-multi-source children of S1 .. Sn

---

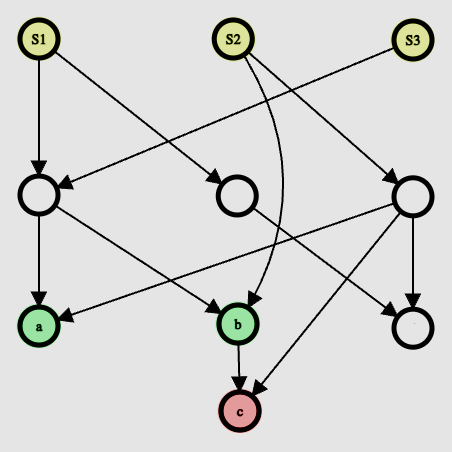
Example: In the following DAG, S1, S2, S3 are the sources. Nodes a, b, c are reachable via all sources. However, node c has a parent which is also reachable via all sources.

So the top view is a, b

---

The naive algorithm for this would be to

1. For each source, find the set of reachable nodes
2. Take the intersection of these sets to find all valid nodes
3. Perform a multi-source BFS from all sources. When moving from parent -> child keep track of whether the parent was a valid node or not. Any valid node which was reached via a parent which is also a valid node gets discarded.

This algorithm takes O((V E) * S) time because of step 1.

V = number of vertices
E = number of edges
S = number of sources

---

Is there a faster algorithm? Can this be done in O(V E)?

CodePudding user response：

Well, you can do this in O(V E) time if you can union sets of size S in constant time.

In the easy case, you would use bitmasks to represent sets, so if S <= 64, for example, then you're good with using a 64-bit word to represent each set, and bitwise-OR for union.

Even if you have a lot more than 64 sources, a compressed set representation with an algorithm like this one is probably going to be your best bet.

The algorithm isn't difficult:

1. Topologically sort the graph, using Kahn's algorithm of DFS;
2. Initialize a set for each vertex. Sources get singleton sets containing only themselves, and other vertexes get empty sets. Also initialize each vertex as "not marked" and "not crossed out";
3. Process the vertexes in topological order. For each vertex, if it's "crossed out", then cross out all of its children. Otherwise replace its set with the union of its set and the sets of all of its parents (which have already been processed). If its set then contains all sources, then mark the vertex and cross out all of its children (which have not yet been processed).
4. Return all the vertexes that are marked.

CodePudding user response：

Step 3 can be optimized.

SET T = valid nodes from step 2
LOOP V over valid nodes
   LOOP P over valid node's parents
      IF P is valid
          DELETE V from T

T is the set of "top nodes"

CodePudding user response：

1. Find the set of reachable nodes for each source.
2. The intersection of the sets of reachable nodes is the set of valid nodes.
3. (all nodes) - (children of valid nodes) is the set of nodes that don't have a valid parent.
4. The intersection of the set of valid nodes with the set of nodes that don't have a valid parent is the answer.

CodePudding user response：

You can "distribute" the data structures by searching from each source in order to label each vertex with the set of sources that reach it. Nodes where the set's cardinality is equal the number of sources are valid. Make a set V of these. Then make one more search of the whole graph removing vertices reached via a valid parent from V. At the end, V contains the answer.

The run time will I think be be O(V * E) assuming constant time set insert and remove. This algorithm takes set intersection out of the picture at the possible cost of more memory.