efficient way of multiplying block diagonal matrix by vector-CodePudding

I have a matrix C structured as following:

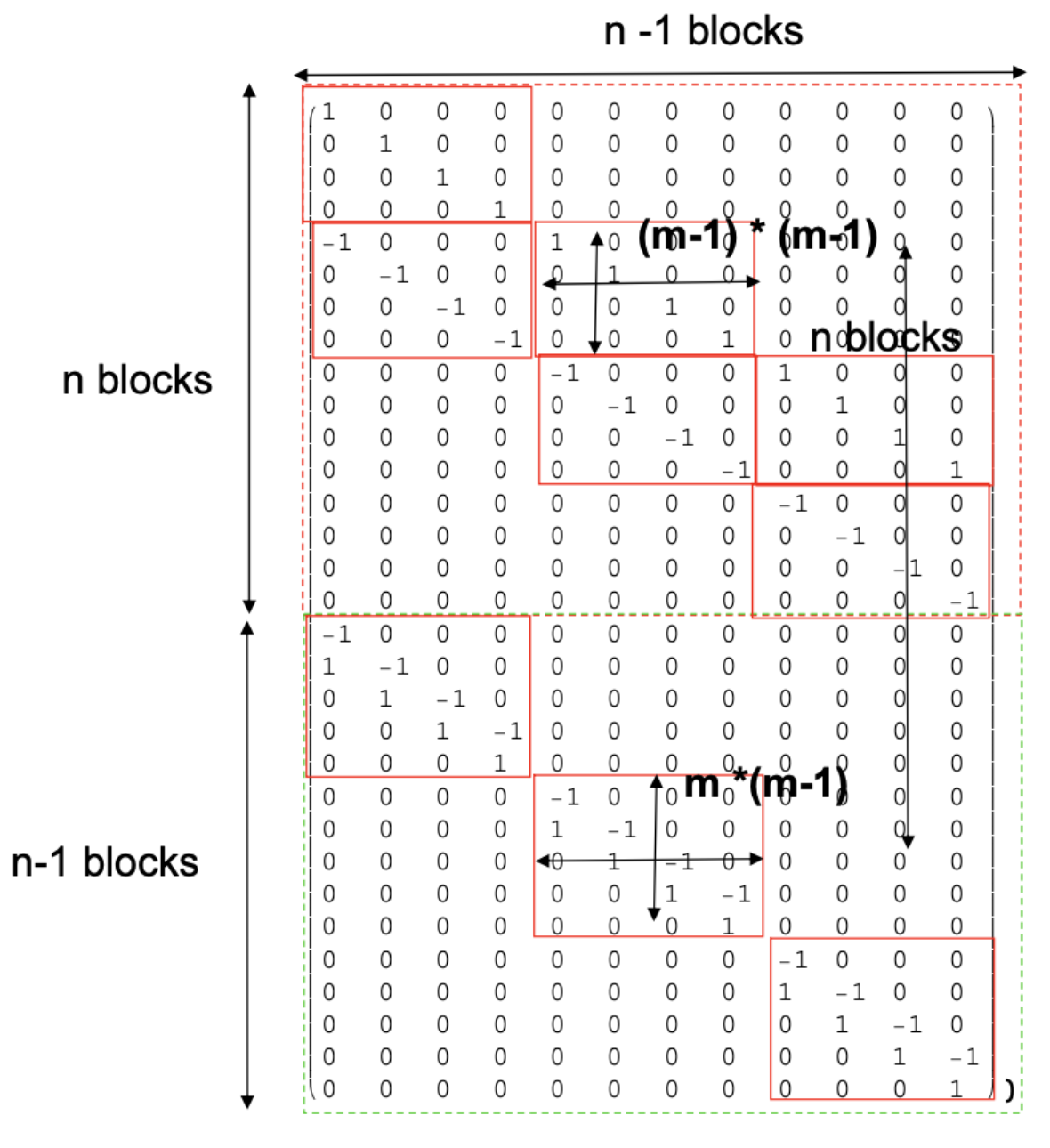
Need to multiply its transpose by vector x.

with the upper part its clear - take slices of the first half of the vector say:

suppose indexation starts at 1.

x1 = x(1:(n-1)*(m-1))

x2 = -x(m:n*(m-1))

then increment partially:

x(1:(n-1)*(m-1)) = x1

x(m:n*(m-1)) =x2

but how to deal with the lower (left after transpose) part? any suggestions?

CodePudding user response：

You can't do it with whole-array operations, so you will need a loop.

integer :: m,n
integer :: x((m-1)*(n-1))
integer :: y((m-1)*n m*(n-1))

integer :: offset, block
integer :: xstart, ystart

offset = n*(m-1)
block = m-1

y = 0
y(:n*block) = y(:n*block)   x
y(m:(n 1)*block) = y(m:(n 1)*block) - x
do i=1,n-1
  xstart = (m-1)*(i-1) 1
  ystart = offset m*(i-1) 1
  y(ystart  :ystart block  ) = y(ystart  :ystart block  ) - x(xstart:xstart block)
  y(ystart 1:ystart block 1) = y(ystart 1:ystart block 1)   x(xstart:xstart block)
enddo