Using R to sample 3 proportion variables so that the three samples add to 1-CodePudding

I have a data set that is split into 3 profiles

Profile 1 = 0.478 (95% confidence interval: 0.4, 0.56)
Profile 2 = 0.415 (95% confidence interval: 0.34, 0.49)
Profile 3 = 0.107 (95% confidence interval: 0.06, 0.15)

Profile 1 Profile 2 Profile 3 = 1

I want to create a stochastic model that selects a value for each profile from each proportion's confidence interval. I want to keep that these add up to one. I have been using

pro1_prop<- rpert (1, 0.4, 0.478, 0.56)              
pro2_prop<- rpert (1, 0.34, 0.415, 0.49)   
pro3_prop<- 1- (pro1_prop   pro2_prop)

But this does not seem robust enough. Also on some iterations, (pro1_prop pro2_prop) >1 which results in a negative value for pro3_prop. Is there a better way of doing this? Thank you!

CodePudding user response：

It is straightforward to sample from the posterior distributions of the proportions using Bayesian methods. I'll assume a multinomial model, where each observation is one of the three profiles.

Say the counts data for the three profiles are 76, 66, and 17.

Using a Dirichlet prior distribution, Dir(1/2, 1/2, 1/2), the posterior is also Dirichlet-distributed: Dir(76.5, 66.5, 17.5), which can be sampled using normalized random gamma variates.

x <- c(76, 66, 17) # observations

# take 1M samples of the proportions from the posterior distribution
theta <- matrix(rgamma(3e6, rep(x   1/2, each = 1e6)), ncol = 3)
theta <- theta/rowSums(theta)
head(theta)
#>           [,1]      [,2]       [,3]
#> [1,] 0.5372362 0.3666786 0.09608526
#> [2,] 0.4008362 0.4365053 0.16265852
#> [3,] 0.5073144 0.3686412 0.12404435
#> [4,] 0.4752601 0.4367119 0.08802793
#> [5,] 0.4428575 0.4520680 0.10507456
#> [6,] 0.4494075 0.4178494 0.13274311

# compare the Bayesian credible intervals with the frequentist confidence intervals
cbind(
  t(mapply(function(i) quantile(theta[,i], c(0.025, 0.975)), seq_along(x))),
  t(mapply(function(y) setNames(prop.test(y, sum(x))$conf.int, c("2.5%", "97.5%")), x))
)
#>            2.5%     97.5%       2.5%     97.5%
#> [1,] 0.39994839 0.5537903 0.39873573 0.5583192
#> [2,] 0.33939396 0.4910900 0.33840295 0.4959541
#> [3,] 0.06581214 0.1614677 0.06535702 0.1682029

If samples within the individual 95% CIs are needed, simply reject samples that fall outside the desired interval.

CodePudding user response：

TL;DR: Sample all three values (for example from a pert distribution, as you did) and norm those values afterwards so they add up to one.

Sampling all three values independently from each other and then dividing by their sum so that the normed values add up to one seems to be the easiest option as it is quite hard to sample from the set of legal values directly.

Legal values:

The downside of my approach is that the normed values are not necessarily legal (i.e. in the range of the confidence intervals) any more. However, for these values using a pert distribution, this only happens about 0.5% of the time.

Code:

library(plotly)
library(freedom)
library(data.table)

# define lower (L) and upper (U) bounds and expected values (E)
prof1L <- 0.4
prof1E <- 0.478
prof1U <- 0.56
prof2L <- 0.34
prof2E <- 0.415
prof2U <- 0.49
prof3L <- 0.06
prof3E <- 0.107
prof3U <- 0.15

dt <- as.data.table(expand.grid(
  Profile1 = seq(prof1L, prof1U, by = 0.002),
  Profile2 = seq(prof2L, prof2U, by = 0.002),
  Profile3 = seq(prof3L, prof3U, by = 0.002)
))

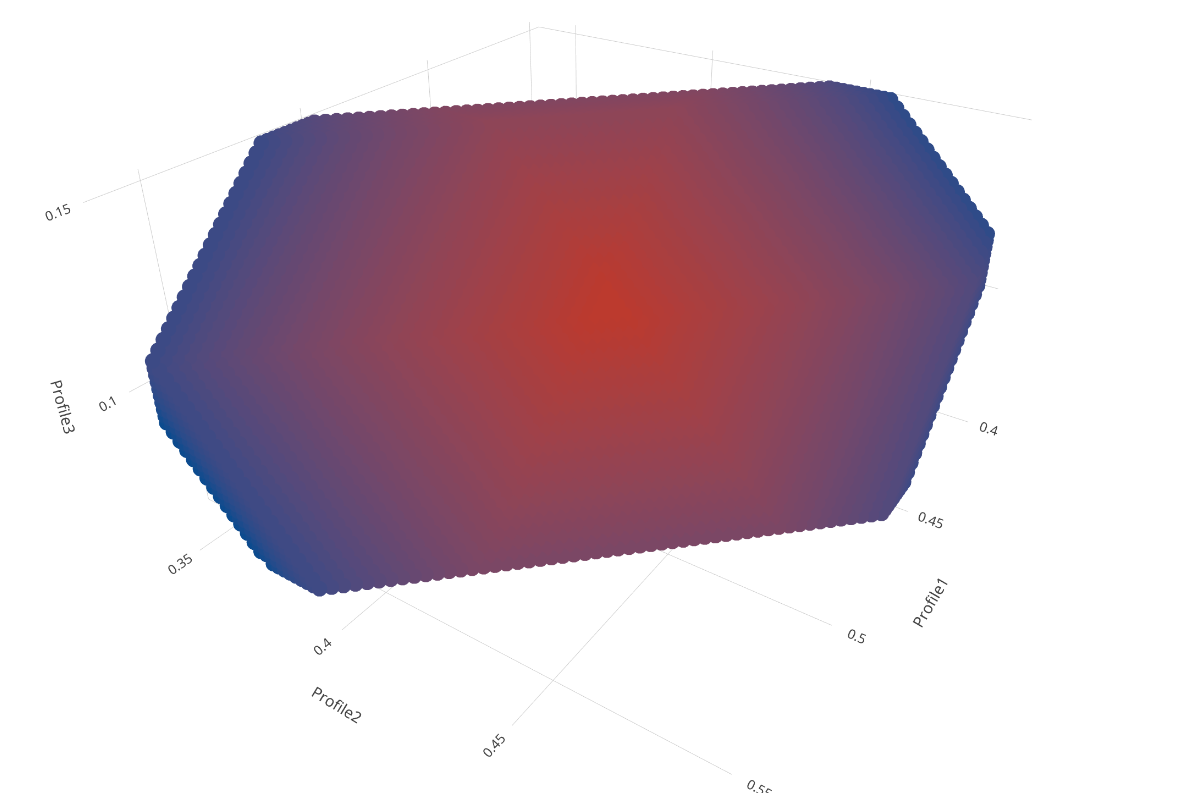
# color based on how far the points are away from the center
dt[, color := abs(Profile1 - prof1E)   abs(Profile2 - prof2E)   abs(Profile3 - prof3E)]
# only keep those points that (almost) add up to one
dt <- dt[abs(Profile1   Profile2   Profile3 - 1) < 0.01]

# plot the legal values
fig <- plot_ly(dt, x = ~Profile1, y = ~Profile2, z = ~Profile3, color = ~color, colors = c('#BF382A', '#0C4B8E')) %>%
  add_markers()
fig

# try to simulate the legal values:
# first sample without considering the condition that the profiles need to add up to 1
nSample <- 100000
dtSample <- data.table(
  Profile1Sample = rpert(nSample, prof1L, prof1U, prof1E),
  Profile2Sample = rpert(nSample, prof2L, prof2U, prof2E),
  Profile3Sample = rpert(nSample, prof3L, prof3U, prof3E)
)

# we want to norm the samples by dividing by their sum
dtSample[, SampleSums := Profile1Sample   Profile2Sample   Profile3Sample]
dtSample[, Profile1SampleNormed := Profile1Sample / SampleSums]
dtSample[, Profile2SampleNormed := Profile2Sample / SampleSums]
dtSample[, Profile3SampleNormed := Profile3Sample / SampleSums]

# now get rid of the cases where the normed values are not legal any more
# (e.g. Profile 1 = 0.56, Profile 2 = 0.38, Profile 3 = 0.06 => dividing by their sum
# will make Profile 3 have an illegal value)
dtSample <- dtSample[
  prof1L <= Profile1SampleNormed & Profile1SampleNormed <= prof1U &
  prof2L <= Profile2SampleNormed & Profile2SampleNormed <= prof2U &
  prof3L <= Profile3SampleNormed & Profile3SampleNormed <= prof3U
]

# see if the sampled values follow the desired distribution
hist(dtSample$Profile1SampleNormed)
hist(dtSample$Profile2SampleNormed)
hist(dtSample$Profile3SampleNormed)

Histogram of normed sampled values for Profile 1: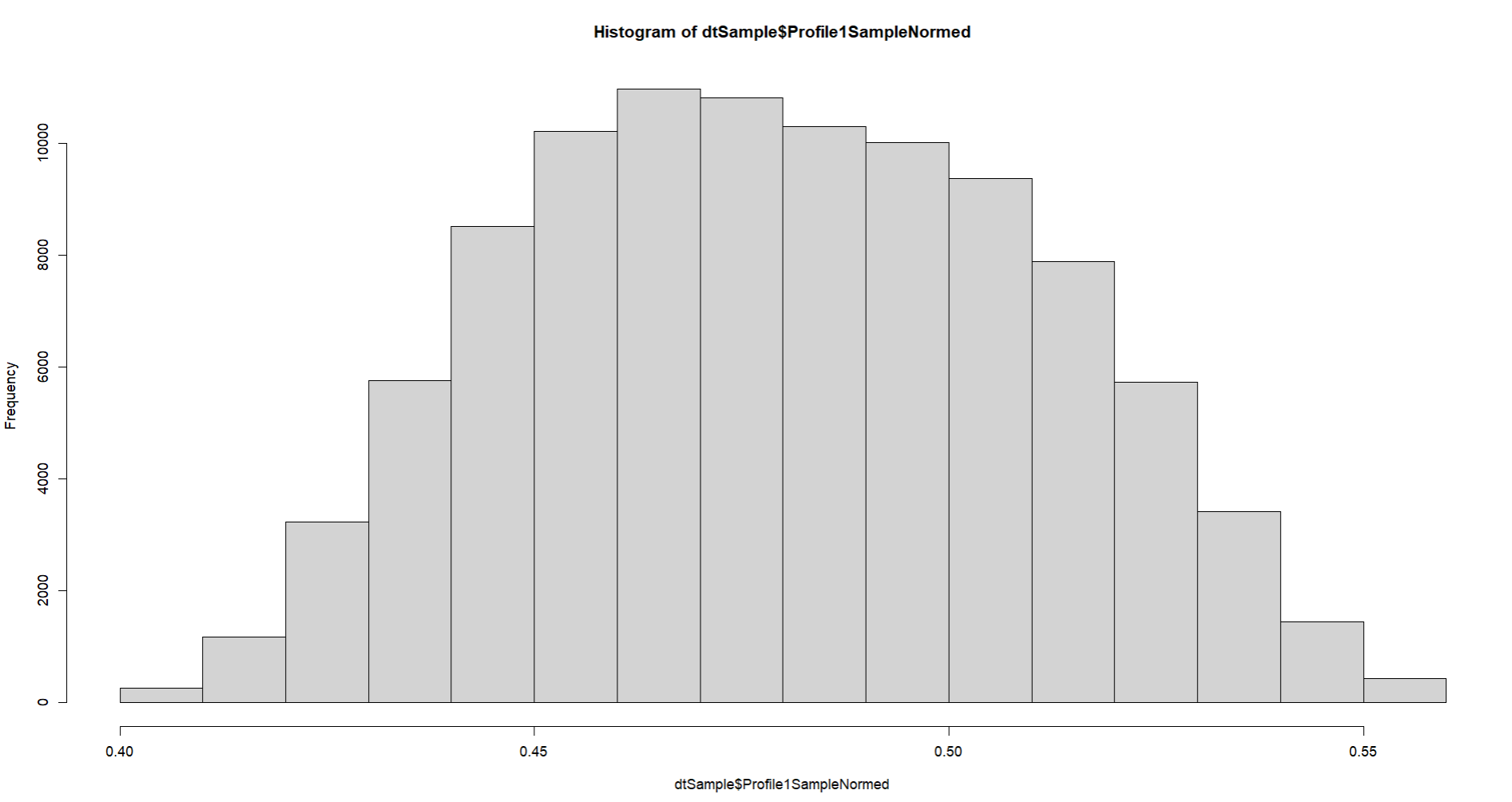

CodePudding user response：

Ok, some thoughts on the matter.

Lets think about Dirichlet distribution, as one providing RV summed up to 1.

We're talking about Dir(a₁, a₂, a₃), and have to find needed a_i.

From the expression for E[X_i]=a_i/Sum(i, a_i), it is obvious we could get three ratios solving equations

a₁/Sum(i, a_i) = 0.478 a₂/Sum(i, a_i) = 0.415 a₃/Sum(i, a_i) = 0.107

Note, that we have only solved for RATIOS. In other words, if in the expression for E[Xi]=a_i/Sum(i, a_i) we multiply a_i by the same value, mean will stay the same. So we have freedom to choose multiplier m, and what will change is the variance/std.dev. Large multiplier means smaller variance, tighter sampled values around the means

So we could choose m freely to satisfy three 95% CI conditions, three equations for variance but only one df. So it is not possible in general.

One cold play with numbers and the code