Gamma Likelihood in R-CodePudding

I want to plot the posterior distribution for data sampled from gamma(2,3) with a prior distribution of gamma(3,3). I am assuming alpha=2 is known. But a graph of my posterior for different values of the rate parameter centers around 4. It should be 3. I even tried with a uniform prior to make things simpler. Can you please spot what's wrong? Thank you.

set.seed(101)
dat <- rgamma(100,shape=2,rate=3)
alpha <- 3
n <- 100
post <- function(beta_1) {
   posterior<- (((beta_1^alpha)^n)/gamma(alpha)^n)*
            prod(dat^(alpha-1))*exp(-beta_1*sum(dat))  
   return(posterior)
}
vlogl <- Vectorize(post)
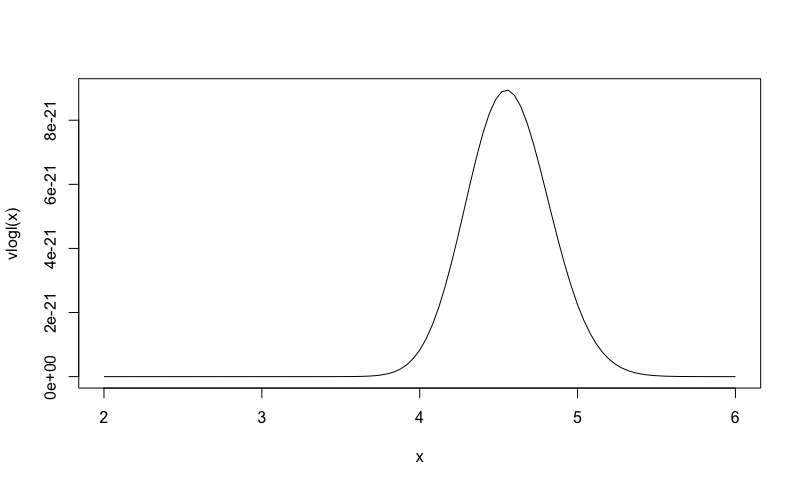
curve(vlogl2,from=2,to=6)

CodePudding user response：

A tricky question and possibly more related to statistics than to programming =). I initially made the same reasoning mistake as you, but subsequently realised to be more careful with the posterior and the roles of alpha and beta_1.

The prior is uniform (or flat) so the posterior distribution is proportional (not equal) to the likelihood.
The quantity you have assigned to the posterior is indeed the likelihood. Plugging in alpha=3, this evaluates to

 (prod(dat^2)/(gamma(alpha)^n)) * beta_1^(3*n)*exp(-beta_1*sum(dat)).

This is the crucial step. The last two terms in the product depend on beta_1 only, so these two parts determine the shape of the posterior. The posterior distribution is thus gamma distributed with shape parameter 3*n 1 and rate parameter sum(dat). As the mode of the gamma distribution is the ratio of these two and sum(dat) is about 66 for this seed, we get a mode of 301/66 (about 4.55). This coincides perfectly with the ``posterior plot'' (again you plotted the likelihood which is not properly scaled, i.e. not properly integrating to 1) produced by your code (attached below).

I hope LifeisBetter now =).

CodePudding user response：

But a graph of my posterior for different values of the rate parameter centers around 4. It should be 3.

The mean of your data is 0.659 (~2/3). Given a gamma distribution with a shape parameter alpha = 3, we are trying to find likely values of the rate parameter, beta, that gave rise to the observed data (subject to our prior information). The mean of a gamma distribution is the shape parameter divided by the rate parameter. 100 observations should be enough to mostly overcome the somewhat informative prior (which had a mean of 1), so we should expect beta to take values somewhere in the region alpha/mean(dat), not 3.

alpha/mean(dat)
#> [1] 4.54915

I'm not going to derive the posterior distribution for beta without TeX, but it is a gamma distribution that includes the rate parameter from the prior distribution of beta (betaPrior = 3):

set.seed(101)
n <- 100
dat <- rgamma(n, 2, 3)
alpha <- 3
betaPrior <- 3

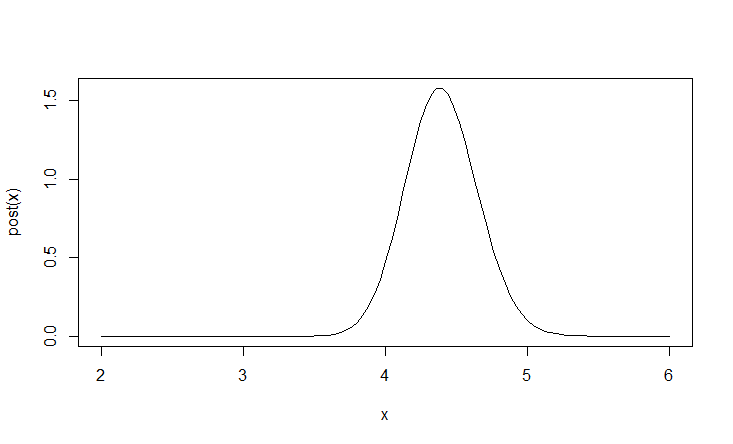
post <- function(x) dgamma(x, alpha*(n   1), sum(dat)   betaPrior)
curve(post, 2, 6)

Notice that the mean of beta is at ~4.39 rather than ~4.55 because of the informative prior that had a mean of 1.