Reverse Isometric Projection in Javascript-CodePudding

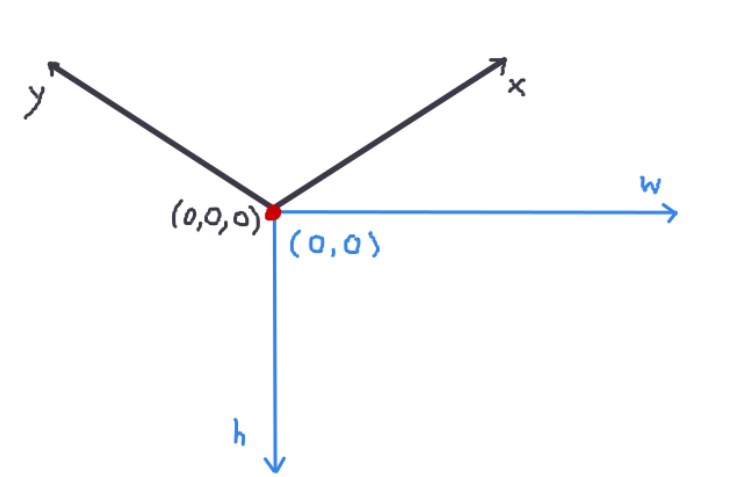
I have a function which converts some 3D coords (x, y, z) into a position in the screen (width, height), with an isometric perspective (true isometric, not dimetric).

Coords_3D_To_2D (x, y, z) {      
   return {
     w: ((x-y) * (Math.sqrt(3)/2)),
     h: (((-x-y) / 2) -z)
   }
 }

So, for better clarification, here we have the blue lines, which represents the 2D Screen, and the black lines, which represents the 3D isometric space:

The above function works fine. If I invoke it like this, for example: Coords_3D_To_2D(15, -10, 5) it returns { w: 21.65, h: -7.5 }, which will be the point projected in the 2D screen (in this case, it would be outside screen, but that doesn't matter).

So the projection 2D -> 3D seems to be working. But what I would like is to have a function which inverts that; it should receive some coords of the 2D Screen (w, h), and also some given value for the z-index, and return the corresponding 3D isometric point.

It should be something like this (here, I assigned a value of 5 for the z-index):

Coords_2D_To_3D (w, h, z = 5) {      
   return {
     x: ?,
     y: ?,
     z: 5
   }
 }

CodePudding user response：

2 equations with 2 variables. Solvable.

function Coords_3D_To_2D(x, y, z) {
  return {
    w: ((x - y) * (Math.sqrt(3) / 2)),
    h: (((-x - y) / 2) - z)
  }
}

console.log(Coords_3D_To_2D(15, -10, 5))

function Coords_2D_and_Z_To_3D(w, h, z) {
  var y = -(h   z   w / Math.sqrt(3))
  var x = 2 * w / Math.sqrt(3)   y
  return {x, y, z}
}

console.log(Coords_2D_and_Z_To_3D(21.650635094610966, -7.5, 5))