confint vs intervals for gls (nlme package) models-CodePudding

There are two methods available to estimate confidence intervals for a gls model in R: using function confint and function intervals. The results are not the same and I want to know what are the causes of the differences and which one is the preferred to use for a gls (and for lme as well) models.

I will use the cats data set for this example. I will use four different approaches to estimate the mean difference (MD) of Hwt between sex:

t-test (heterogeneous variance)
Linear model, using lm (homogeneous variance)
Linear model, using gls (homogeneous variance)
Heteroscedastic linear model, using gls (heterogeneous variance)

for the gls approaches confint and intervals are available for calculating confidence intervals. Here is the code:

library(pacman)
p_load(tidyverse)
p_load(MASS)
p_load(nlme)

set.seed(150)

cats%>%ggplot(aes(x=Sex,y=Hwt)) 
  geom_boxplot() theme_bw()

###different approaches for the same mean difference estimation
cats_ttest<-t.test(Hwt~Sex,data=cats)
cats$Sex<-relevel(cats$Sex,ref="M")
cats_lm<-lm(Hwt~Sex,data=cats)
cats_gls_hom<-gls(Hwt~Sex,data=cats)
cats_gls_het<-gls(Hwt~Sex,weights=varIdent(form=~1|Sex),data=cats)

###store estimations and CI's from different approaches
a<-rbind(confint(cats_lm),confint(cats_gls_hom),confint(cats_gls_het),
         intervals(cats_gls_hom,which = "coef")$coef[,c(1,3)],
         intervals(cats_gls_het,which = "coef")$coef[,c(1,3)]) %>% data.frame%>% {cbind(par=rownames(.),.)}
a$par<-a$par %>% str_remove_all("X.|.1|.2|.3|.4")
a$par<-factor(a$par,levels =c("Intercept.","SexF"),
              labels =c("Intercept.","SexF") )

a$est<-c(rep(cats_lm %>% coef,3),
         cats_gls_hom %>% coef,cats_gls_het %>% coef
         )
a$mod<-c(rep("cats_lm_ci",2),rep("cats_gls_hom_ci",2),rep("cats_gls_het_ci",2),
         rep("cats_gls_hom_int",2),rep("cats_gls_het_int",2)
         )
colnames(a)[2:3]<-c("LCI","UCI")
a<-rbind(data.frame(par="SexF",LCI=cats_ttest$conf.int[1],
                    UCI=cats_ttest$conf.int[2],est=cats_ttest$estimate[1]-cats_ttest$estimate[2],
                    mod="ttest"),a)
a$mod<-factor(a$mod,levels =c("ttest","cats_lm_ci","cats_gls_hom_ci","cats_gls_het_ci","cats_gls_hom_int","cats_gls_het_int"))
a$diff<-a$UCI-a$LCI
rownames(a)<-NULL

###results
a[order(a$par,a$diff),]
#>           par       LCI       UCI       est              mod      diff
#> 4  Intercept. 10.879181 11.766179 11.322680  cats_gls_hom_ci 0.8869980
#> 2  Intercept. 10.875369 11.769992 11.322680       cats_lm_ci 0.8946223
#> 8  Intercept. 10.875369 11.769992 11.322680 cats_gls_hom_int 0.8946223
#> 6  Intercept. 10.816754 11.828606 11.322680  cats_gls_het_ci 1.0118521
#> 10 Intercept. 10.812406 11.832955 11.322680 cats_gls_het_int 1.0205495
#> 7        SexF -2.758218 -1.482888 -2.120553  cats_gls_het_ci 1.2753295
#> 11       SexF -2.763699 -1.477407 -2.120553 cats_gls_het_int 1.2862917
#> 1        SexF -2.763753 -1.477352 -2.120553            ttest 1.2864011
#> 5        SexF -2.896844 -1.344261 -2.120553  cats_gls_hom_ci 1.5525835
#> 3        SexF -2.903517 -1.337588 -2.120553       cats_lm_ci 1.5659288
#> 9        SexF -2.903517 -1.337588 -2.120553 cats_gls_hom_int 1.5659288

a %>% ggplot(aes(x=par,y=est,color=mod,group=mod)) geom_point(position=position_dodge(0.5)) 
  geom_errorbar(aes(ymin=LCI, ymax=UCI), width=.2,
                position=position_dodge(0.5)) theme_bw()

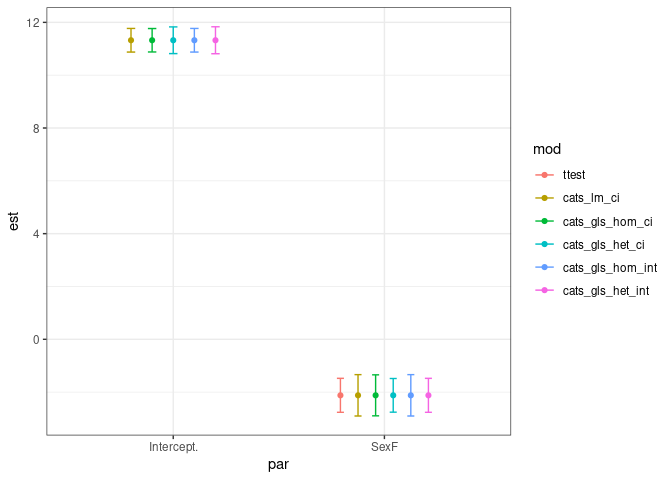
^{Created on 2022-09-11 by the reprex package (v2.0.1)}

As you can see, there are mild differences in CI amplitudes from the different methods,and as expected, the methods which accounts for differences in variances produced the narrowest CI for the mean differences (parameter SexF in dataframe a).

So, why are two methods available to estimate confidence intervals for gls models, what are the differences between them and which one is the preferred one for this kind of models?

CodePudding user response：

tl;dr use intervals(), it gives you CIs based on a Student-t rather than a Normal sampling distribution.

If you look at methods(class = "gls") you'll see that confint() is not listed. That means that when you call confint(gls_fit), R falls back to the default confint method. If we look at the code for stats::confint.default you'll see fac <- qnorm(a); ...; ci[] <- cf[parm] ses %o% fac. In other words, confint.default is constructing CIs based on a Normal distribution.

In contrast, nlme:::intervals.gls uses

 len <- -qt((1 - level)/2, dims$N - dims$p) * sqrt(diag(object$varBeta))

— i.e., an interval based on a t-distribution.

It makes very little difference in this case (CI interval width of 1.55 vs 1.56).

For what it's worth, you can streamline this kind of comparison a little bit using broom/broom.mixed (although this does not include the confint.default option for gls!)

library(broom)
library(broom.mixed)
options(pillar.sigfig = 7)
(tibble::lst(cats_ttest, cats_lm, cats_gls_hom, cats_gls_het)
    |> map_dfr(tidy, .id = "model", conf.int = TRUE)
    ## t-test doesn't have a "term" element
    |> mutate(across(term, ~ifelse(is.na(.), "SexF", term)))
    |> select(model, term, estimate, lwr = conf.low, upr = conf.high)
    |> mutate(width = upr - lwr)
    |> arrange(term)
)

As a general rule, you should use the most specific method available — this usually happens automatically, it's sort of an accident that confint() works for gls objects (partly because the nlme package predates R itself, so doesn't follow all of its conventions ...)