Compute size of rose tree in Haskell-CodePudding

For an exercise for uni I have to work with rose trees in Haskell, defined as such:

data Rose a = MkRose a [Rose a]

One of the exercises is writing a function size :: Rose a -> Int returning the number of nodes for a given tree. The solution I found for this exercise (also on StackOverflow "https://stackoverflow.com/questions/56060053/write-a-function-that-counts-the-number-of-elements-in-a-rosetree") is the following:

size (MkRose _ []) = 1
size (MkRose a (t:ts)) = roseSize t   roseSize (MkRose a ts)

But I dont really understand why this is correct. Say you have the following rose tree:

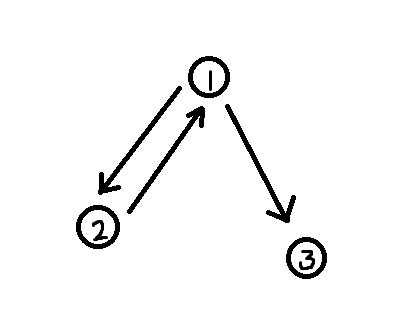
Does it not miscount the number of nodes. You start from node 1, where t = MkRose 2 [MkRose 1 (t:ts)] and ts = MkRose 3 []. Now the size of MkRose 1 ts is two. and the size of t is two aswell. Giving the final answer 4, when clearly there are 3 nodes. Does anyone know where I am mistaken? Thanks in advance!!

CodePudding user response：

No, it does not give an incorrect answer for the tree you described^* -- indeed, it does not give an answer at all. Let us define

t = Rose 2 [Rose 1 [t, Rose 3 []]]

and then compute:

size t
= { unroll defn. of t }
size (Rose 2 [Rose 1 [t, Rose 3 []]])
= { defn. of size, case 2 }
size (Rose 1 [t, Rose 3 []])   size (Rose 2 [])
= { defn. of size, case 2 }
size t   size (Rose 1 [Rose 3 []])   size (Rose 2 [])

But this first addend, size t, is exactly the thing we started out to compute! So we have entered a loop, and will endlessly expand to larger and larger sums.

^* The tree you described and the graph you drew do not represent the same thing. While t as defined above will be stored in memory like the graph you drew when using GHC (and probably most sane implementations), its meaning is an infinite tree that looks something like this:

2 --> 1 --> 2 --> 1 --> 2 --> 1 --> 2 --> 1 --> 2 --> ...
      |           |           |           |
      v           v           v           v
      3           3           3           3