Is there a faster way to solve the following problem?-CodePudding

A is a mn matrix
B is a nn matrix

I want to return matrix C of size m*n such that:
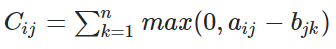
$C_{ij} = \sum_{k=1}^{n} max(0, a_{ij} - b_{jk})$

In python it could be like below

for i in range(m):
   for j in range(n):
      C[i][j] = 0
      for k in range(n):
         C[i][j]  = max(0, A[i][j] - B[j][k])

this runs on O(m*n^2) but it is possible to lower that? I think some divide and conquer algorithms might help here but I am not familiar with them.

CodePudding user response：

For each j, You can sort each column B[j][:] and compute cumulative sums.

Then for a given A[i][j] you can find the sum of B[j][k] that are larger than A[i][j] in O(log n) time using binary search. If there's x elements of B[j][:] that are greater than A[i][j] and their sum is S, then C[i][j] = A[i][j] * x - S.

This gives you an overall O((m n)n log n) time algorithm.

CodePudding user response：

I would look on much simpler construct and go from there..

lets say the max between 0 and the addition wasn't there.

so the answer would be : c(i,j)n - sum(b(j,) on this you could just go linearly by sum each vector and erase it from c(i,j)n and because you need sum each vector in b only once per j it can be done in max(mn,nn)

now think about simple solution for the max problem... if you would find which elements in b(j,) is bigger than c(i,j) you could just ignore their sum and substract their count from the multipication of c(i,j)

All of that can be done by ordering the vector b(j,) by size and make a summing array to each vector from the biggest to lowest (it can be done in nnlog(n) because you order each b(j,) vector once)

then you only need to binary search where is the c(i,j) in the ordered vector and take the sum you already found and subtract it from c(i,j) * the position you found in the binary search.

Eventually you'll get O( max( mnlog(n),nnlog(n) ) )