Generate half sine in matlab-CodePudding

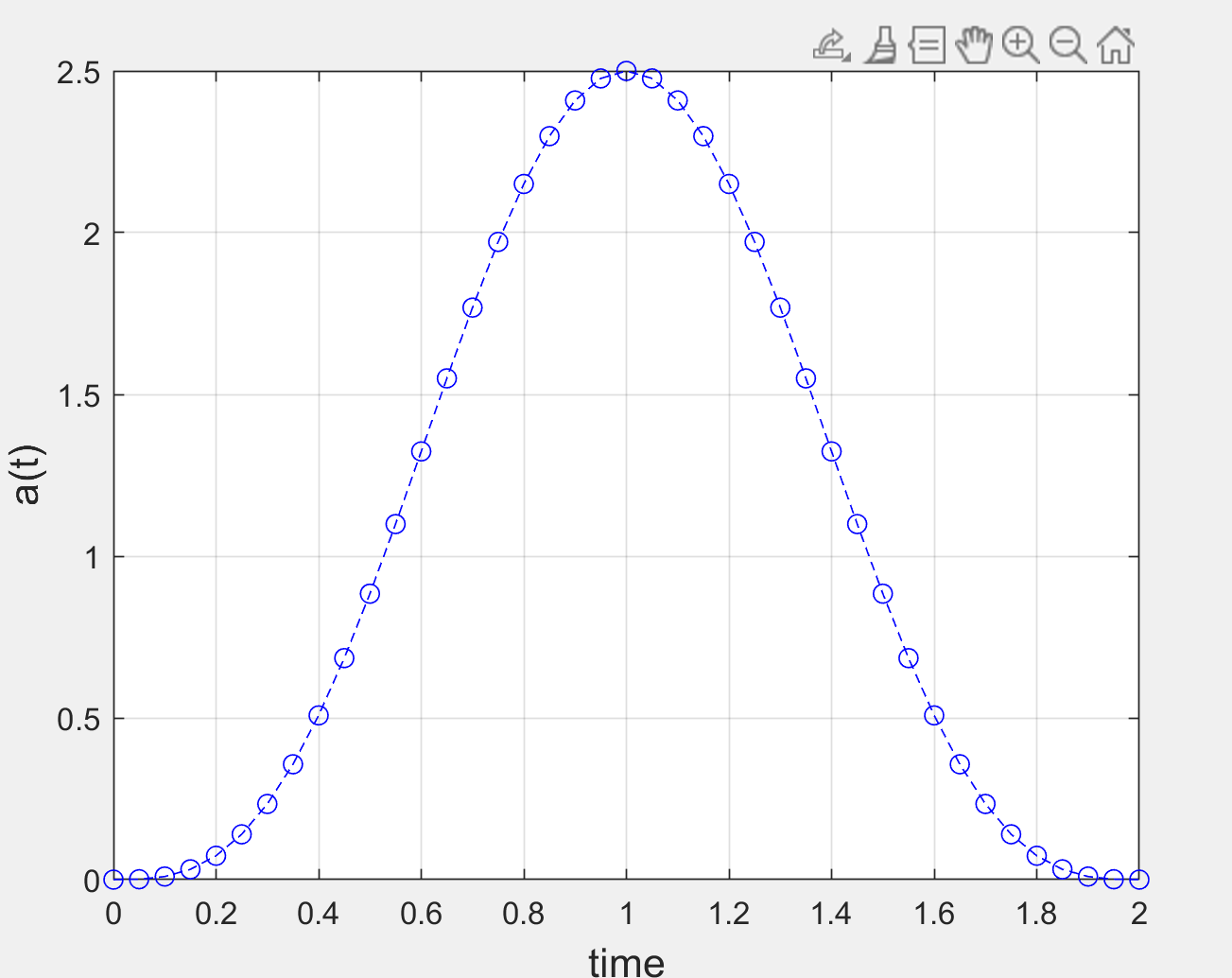
I have half a sine with time 0:2*T:

Rc = 1e3;      
T = 1/Rc;      
Fs = 2e3;      % sampling frequency
dt = 1/Fs;
over = Fs/Rc;   % sampling factor - 2
sps = 10;  
time = 0:dt/sps:2*T;
half_Sine = sin(pi*time/(2*T)).^3; 
figure(1);
plot(time,half_Sine, 'b--o');
grid on
 xlabel('time','FontSize',13); 
ylabel('a(t)','FontSize',13);

But i need time -T/2<= time<= T/2. And represent the time axis as time/T. When i do

time = -T/2:dt/sps:T/2;

This gives me not half a sine. So I need something like this:

CodePudding user response：

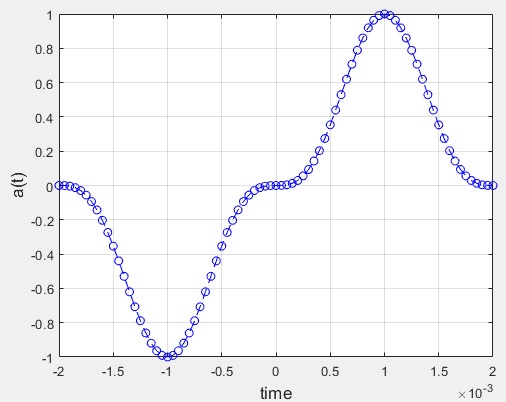
1.- the cube on the sin function prevents the resulting plot from having y axis symmetry.

Rc = 1e3;      
T = 1/Rc;      
Fs = 2e3;      % sampling frequency
dt = 1/Fs;
over = Fs/Rc;   % sampling factor - 2
sps = 10;  
t =-2*T :dt/sps:2*T;
y= sin(pi*t/(2*T)).^3; 
figure;
plot(t,y, 'b--o');
grid on
xlabel('time','FontSize',13); 
ylabel('a(t)','FontSize',13);

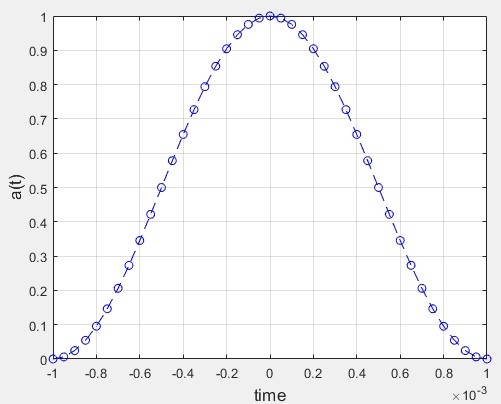
2.- To have max on t=0 you need to use cos function , not sin, and square, not cube

Rc = 1e3;      
T = 1/Rc;      
Fs = 2e3;      % sampling frequency
dt = 1/Fs;
over = Fs/Rc;   % sampling factor - 2
sps = 10;  
t =-T :dt/sps:T;
y= cos(pi*t/(2*T)).^2; 
figure(1);
plot(t,y, 'b--o');
grid on
xlabel('time','FontSize',13); 
ylabel('a(t)','FontSize',13);

Now you have [-T T] plot,

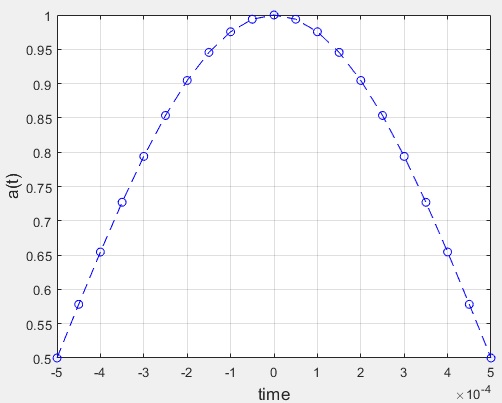
3.- the interval you need is [-T/2 T/2]

t = -T/2:dt/sps:T/2; y= cos(pit/(2T)).^2;

figure; plot(t,y, 'b--o'); grid on xlabel('time','FontSize',13); ylabel('a(t)','FontSize',13);

4.- You mention you want to normalise the time axis.

If you modify t dividing by T the resulting plot is going to be a really narrow time span around t=0 and nearly constant y=1.

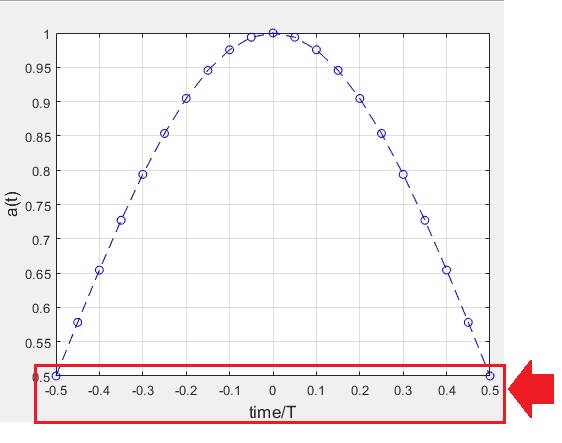
Instead, just modify the x axis anotation in the following way

figure;
hp1=plot(t,y, 'b--o');
hp1.XData=hp1.XData/T
grid on
xlabel('time/T','FontSize',13); 
ylabel('a(t)','FontSize',13);

Hey, thanks for reading my answer.

If this solves your question would you please be so kind to consider clicking on the accepted answer.