In a SAT problem, how can I prove my algorithm in polinomyal time is valid for all SAT problem?-CodePudding

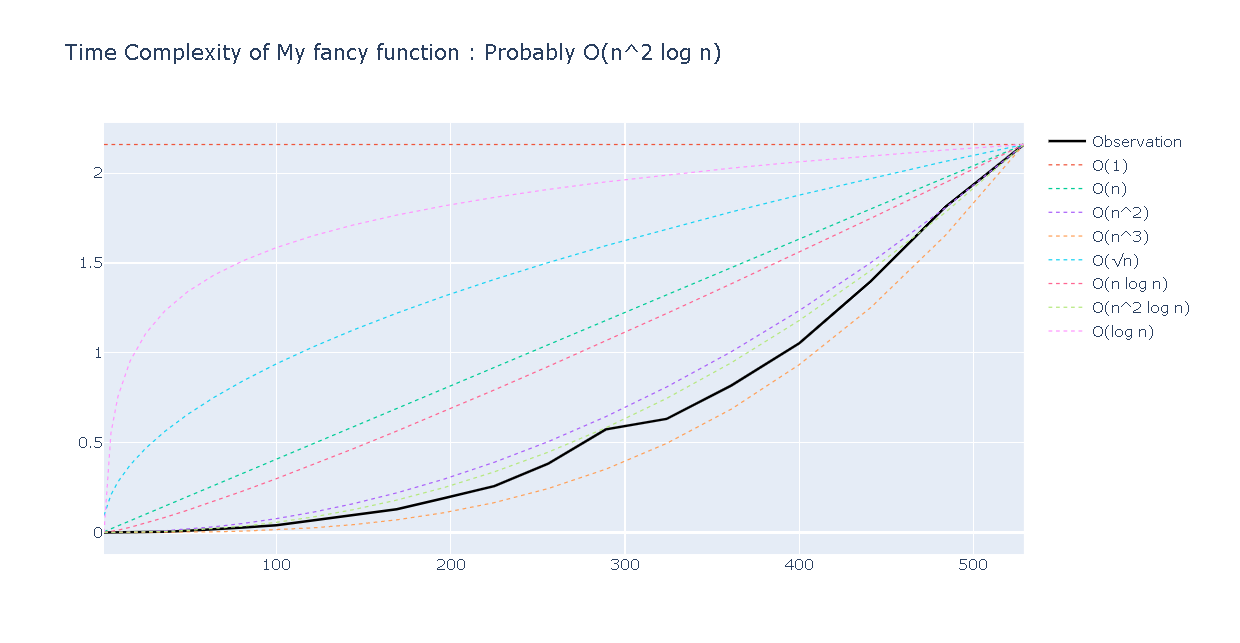
I work on a algo for SAT resolution and actually after a comparison my algo has a complexity of O(n^3) in approximate worst scenario. How can prove it valid for all SAT problem ? The test is for SAT-1 to SAT-100 comparison for row and column in row between 1 and 100 with negative value possible.

plot

CodePudding user response：

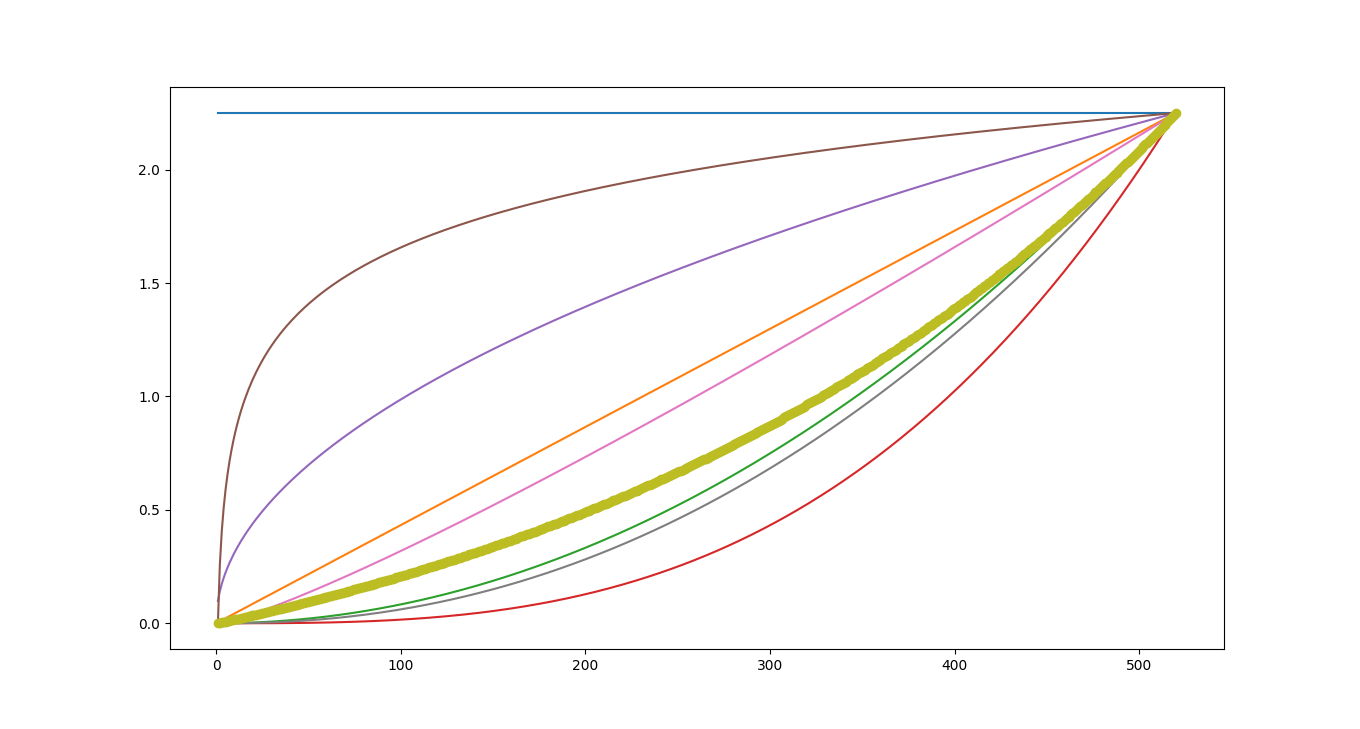
From your curve fitting method, how would your characterize the complexity shown by the thick curve here (all the others are the same as in your chart)

Spoiler alert: it's an exponential.

Moral: curve fitting proves nothing.

CodePudding user response：

Here I post an alorithmical big O representation of my algorithm, can you provide me what is that complexity with it ?

N
    if C:
        C
    N
        if C:
            C
        if N:
            C
    if C:
        C

N*N*N*N

N*N

N*N


N
    if C:
        N
    
    N * N

    N
        N
            log n ** 2
            C
            if N:
                N:
                    N


    N
        N
            log n ** 2

            if C:
                N
                    C
            else:
                C

    if N * (n log n):

        if C:
            N
        else:
            if C:
                N
                N
    else:
        N * (n log n)
        C
    if C:
        C
    else:
        N*N