Problem
I need to get the intersection point of two curves several times. Given two dataframes as the following:

      name   flow  head
1       a     1     9
2       a     2     5
3       a     3     1
4       b     1     40
5       b     2     30
6       b     3     10
7       c     1     15
8       c     2     9
9       c     3     1

As you can see, "a" is a different curve from "b" and so on, but they all share the same x-axis. The second dataset is one simple curve:

      flow  system_head
1       1        1.2
2       2        5.6
3       3        9.5
4       4        17

Sample resulting dataframe
What I want to discover is a way to find the intersection between "head" and "system_head" for every different name:

      name   closest_flow_point  index_intersection_point
1       a           2                       2
2       b           3                       6
3       c           2                       8

I have been able to get the closest intersection value between two different columns with the following line of code:

idx = np.argwhere(np.diff(np.sign(df["head"] - df2["system_head"]))).flatten()

but this doesn't work when I have multiple curves (e.g: curves "a", "b" and "c").

I have also been able to separate the "name" in different dataframes with a loop:

names = df["name"].unique()
for name in names:
    df_test = df.loc[df["name"] == name, :]

and while this does work in separating, I can't proceede from here.

It's also important to mention that there is no exact match for the columns ["head"] and ["system_head"] (which means that I can't use pd.where or pd.loc), and the dataframe has over a million rows.

To help visualize,

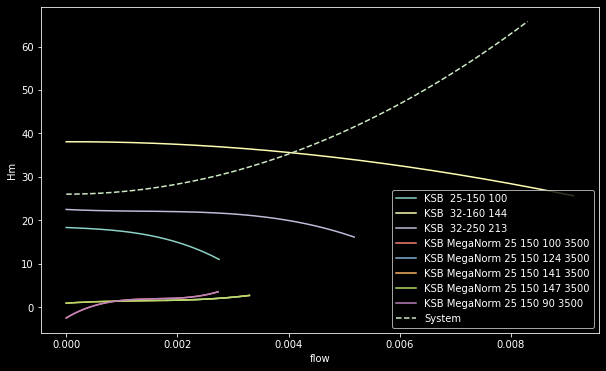
We see that only KSB 32-160 144 intersects the system curve. How we are going to identify the intersection points require some finesse.

1

If we assume that the system curve has a y-value whenever an individual curve has a y-value, we can simply merge them on the x-axis (flow):

tmp = (
    pd.merge(df, df_system, on="flow", suffixes=("", "_system"))
    .assign(is_equal=lambda x: np.abs(x["Hm"] - x["Hm_system"]) < 0.01) # find a threshold that suits your requirements
)

This is enough to give us some info about the intersection points:

tmp[tmp["is_equal"]]

                  name      flow        Hm  Hm_system  is_equal
18570  KSB  32-160 144  0.004061  35.52770  35.522806      True
18572  KSB  32-160 144  0.004062  35.52644  35.527495      True
18574  KSB  32-160 144  0.004063  35.52518  35.532185      True

But instead of a single point, the algorithm found 3 consecutive points that intersect the system curve! We can refine this a little bit by implementing a rule: if consecutive points intersect the system curve, we will take the mean flow of those points:

intersects = {}
for name, sub_df in tmp.groupby("name"):
    is_equal = sub_df["is_equal"]
    if is_equal.sum() == 0:
        continue

    sub_df["island"] = is_equal.ne(is_equal.shift()).cumsum()
    intersects[name] = sub_df[is_equal].groupby("island")["flow"].mean().to_list()

# intersects: {'KSB  32-160 144': [0.004062]}
# 0.004062 is the `flow` value of the intersection point

2

A more advanced scenario is that the system curve may not have some flow values present in the individual curve. If you refer back to the chart, you can see that the system curve looks pretty much like a quadratic curve, so let's try some curve fitting:

poly, residuals, *_ = np.polyfit(df_system["flow"], df_system["Hm"], deg=2, full=True)

# poly: array([5.77047893e 05, 1.54957651e 00, 2.60000005e 01])
# residuals: array([9.45696098e-13])

This is an extremely good fit as the residuals are near 0. So we can use poly to interpolate the system curve value at any point:

tmp = (
    df.assign(Hm_system=np.polyval(poly, df["flow"]))
    .assign(is_equal=lambda x: np.abs(x["Hm"] - x["Hm_system"]) < 0.01)
)

And you can apply the same algorithm above to identify the intersection points.