How to plot a plane perpendicular to a given normal and position in 3D in matplotlib?-CodePudding

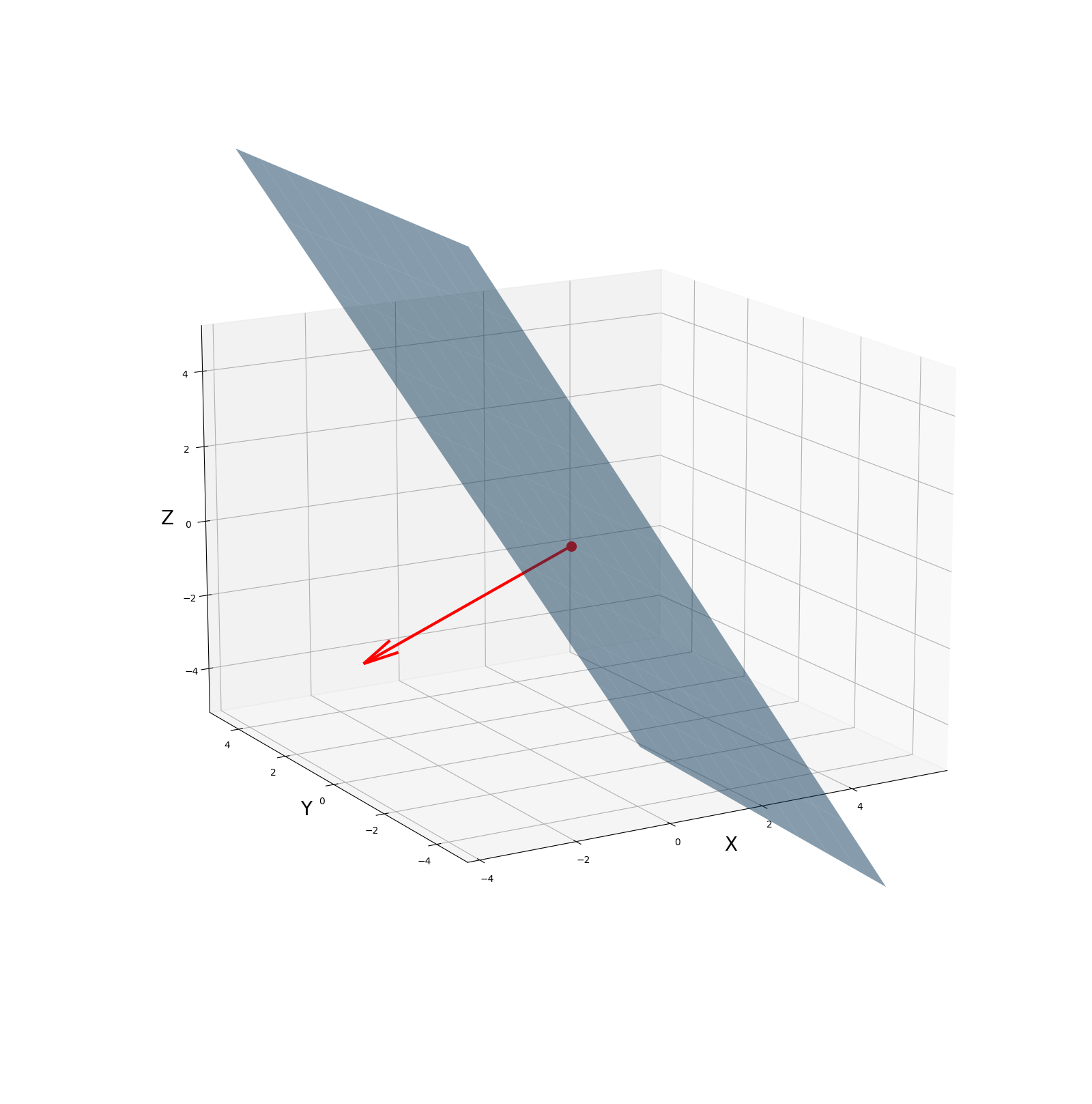
For example, Let A be the x,y,z coordinate positions and N_A be the normal. I need to plot a plane perpendicular to the normal with the normal arrow pointing in 3D

A = [0.960396491, 0.06136547597, -6.718505E-5]
N_A = [ -0.89169092,  0.02074738, -0.45216906]

CodePudding user response：

The plot_surface method allows you to plot a surface given xx, yy, zz meshes. So the name of the game is creating these meshgrid objects.

A normal (a, b, c) specifies a plane via the relationship: ax by cz d = 0, where we can determine d given a point (x, y, z) on the plane through simple arithmetic. Given arbitrarily chosen xx and yy meshgrid objects, we can then solve for z to compute the corrsponding zz meshgrid, and plot.

import numpy as np
import matplotlib.pyplot as plt

point  = np.array([ 0.960396491, 0.06136547597, -6.718505E-5])
normal = np.array([-0.891690920, 0.02074738000, -0.45216906])

# A plane is given by
# a*x   b*y   c*z   d = 0
# where (a, b, c) is the normal.
# If the point (x, y, z) lies on the plane, then solving for d yield:
# d = -(a*x   b*y   c*z)
d = -np.sum(normal * point)

# Create a meshgrid:
delta = 5
xlim = point[0] - delta, point[0]   delta
ylim = point[1] - delta, point[1]   delta
xx, yy = np.meshgrid(np.arange(*xlim), np.arange(*ylim))

# Solving the equation above for z:
# z = -(a*x   b*y  d) / c
zz = -(normal[0] * xx   normal[1] * yy   d) / normal[2]

fig = plt.figure()
ax = fig.add_subplot(projection='3d')
ax.plot_surface(xx, yy, zz, alpha=0.5)

# Plot point.
x, y, z = point
ax.plot(x, y, z, marker='o', markersize=10, color='red')

# Plot normal.
dx, dy, dz = delta * normal
ax.quiver(x, y, z, dx, dy, dz, arrow_length_ratio=0.15, linewidth=3, color='red')

# Enforce equal axis aspects so that the normal also appears to be normal.
ax.set_xlim(*xlim)
ax.set_ylim(*ylim)
zlim = point[2] - delta, point[2]   delta
ax.set_zlim(*zlim)

# Label axes.
ax.set_xlabel('X', fontsize=20)
ax.set_ylabel('Y', fontsize=20)
ax.set_zlabel('Z', fontsize=20)

plt.show()