Unexpected behavior for contourplot in polar coordinates

I wish to plot a bunch of points onto a polar plot. When I apply it with simulated data, it works. When I try the same with my real data it fails and I'm not sure why.

# First with simulated data

# The angles for each point
phi = np.linspace(0, math.pi*2, 40) # full circle
phi = np.concatenate([phi, phi, phi, phi]) # 4 full circles
# The radii
rho = np.array([0,1,2,3]) # the radii for each circle
rho = np.repeat(rho, 40)

assert phi.shape == rho.shape

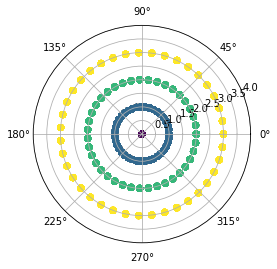
# First just plot the points
plt.figure()

ax = plt.subplot(111, projection='polar')
ax.scatter(phi, rho, c=rho)

ax.set_ylim(0,4)

This appears to work. Next, I use the following to draw concentric contours around the origin. The Z property is set to the radii, i.e., points that equally far away from the origin should be grouped within a contour.

# Create a meshgrid from the points
X, Y = np.meshgrid(phi, rho)

plt.figure()

ax = plt.subplot(111, projection='polar')
ax.scatter(X, Y, c=Y)
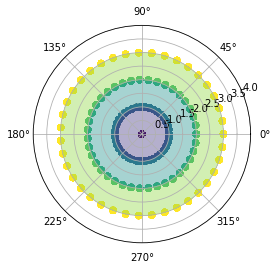
CS = ax.contourf(X,Y, Y, 2, alpha=0.4)

ax.set_ylim(0,4)

This works exactly as I want it:

Next, I want to apply this to my real data. My actual data has millions of data points, but here's just a small sample to reproduce.

rho = np.array([0.38818333, 0.73367091, 0.42336148, 1.39013061, 0.31064486,0.34546275, 0.05445943, 0.85551576, 0.55174167, 1.42371249,0.17644804, 1.76221456, 0.64519126, 0.02408941, 1.43986863,0.72718428, 0.4262945 , 0.1355583 , 0.86319986, 0.71212376,0.14891707, 1.01624534, 1.26915981, 1.39384488, 0.09623481,0.92635469, 1.74757901, 0.15811954, 0.22052651, 0.30784166,0.92740352, 1.29621377, 0.29832842, 1.04442307, 1.36185399,0.42979785, 0.94402815, 0.3786981 , 0.75865969, 1.97273479,0.61140136, 0.71452862, 0.25793468, 1.1751275 , 1.53945948,0.64150917, 0.09274101, 0.52548715, 0.7932458 , 0.90292444])
phi = np.array([1.04208195, 4.67055389, 3.32909655, 1.18709268, 0.86036178,5.820191  , 4.30457004, 1.81242968, 0.64295926, 4.85684143,2.73937709, 3.22891963, 0.25822595, 0.69526782, 0.70709764,1.92901075, 3.44538869, 5.38541473, 0.95255568, 4.01519928,0.8503274 , 5.26774545, 4.07787945, 4.51718652, 0.3170884 ,2.1946835 , 3.12550771, 5.67275731, 1.0000195 , 1.82570239,5.62578391, 0.81923255, 2.00131474, 0.48190872, 4.78875363,5.60395833, 2.01674743, 2.13494958, 5.10829845, 0.95324309,1.59531506, 4.99145225, 6.19873491, 3.32802456, 1.15590926,0.52989939, 6.02205398, 3.66013508, 4.16276819, 2.60498467])

assert rho.shape == phi.shape # both are (50,)

plt.figure()
ax = plt.subplot(111, projection='polar')

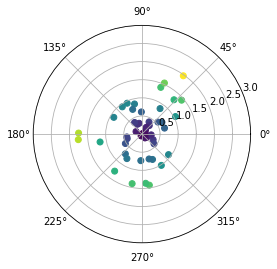
ax.scatter(phi, rho, c=rho)
ax.set_ylim(0,3)

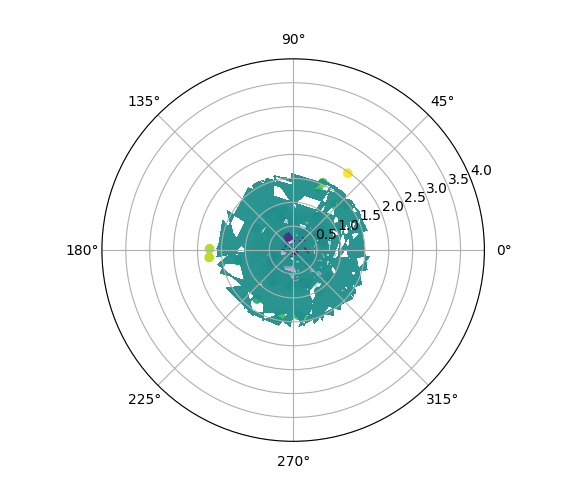
Of course, my real data has much more variation that the simulated circles above. Next, I try to draw the contours in the same method. However, this now fails:

# Create a meshgrid from the points
X, Y = np.meshgrid(phi, rho)

plt.figure(figsize=(10,10)) # a little bigger to see better

ax = plt.subplot(111, projection='polar')
ax.scatter(X, Y, c=Y)
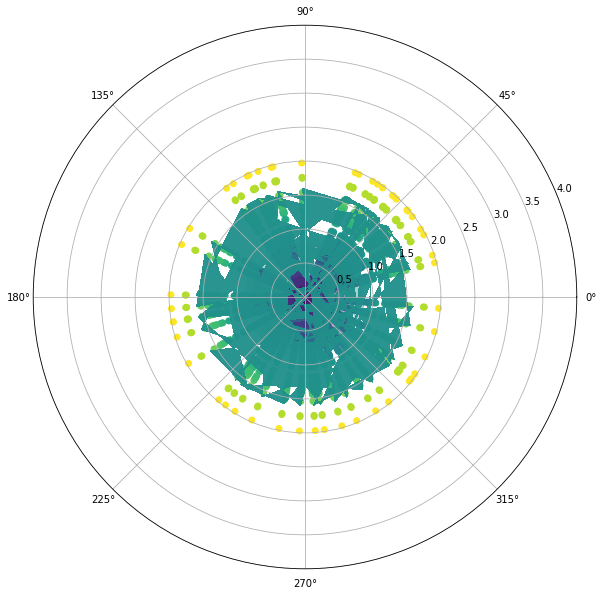
CS = ax.contourf(X,Y, Y, 2, alpha=0.4)

ax.set_ylim(0,4)

CodePudding user response：

This behaviour is due to the fact that rho and phi are not sorted. Let's see:

import matplotlib.pyplot as plt
import numpy as np

rho = np.array([0.38818333, 0.73367091, 0.42336148, 1.39013061, 0.31064486,0.34546275, 0.05445943, 0.85551576, 0.55174167, 1.42371249,0.17644804, 1.76221456, 0.64519126, 0.02408941, 1.43986863,0.72718428, 0.4262945 , 0.1355583 , 0.86319986, 0.71212376,0.14891707, 1.01624534, 1.26915981, 1.39384488, 0.09623481,0.92635469, 1.74757901, 0.15811954, 0.22052651, 0.30784166,0.92740352, 1.29621377, 0.29832842, 1.04442307, 1.36185399,0.42979785, 0.94402815, 0.3786981 , 0.75865969, 1.97273479,0.61140136, 0.71452862, 0.25793468, 1.1751275 , 1.53945948,0.64150917, 0.09274101, 0.52548715, 0.7932458 , 0.90292444])
phi = np.array([1.04208195, 4.67055389, 3.32909655, 1.18709268, 0.86036178,5.820191  , 4.30457004, 1.81242968, 0.64295926, 4.85684143,2.73937709, 3.22891963, 0.25822595, 0.69526782, 0.70709764,1.92901075, 3.44538869, 5.38541473, 0.95255568, 4.01519928,0.8503274 , 5.26774545, 4.07787945, 4.51718652, 0.3170884 ,2.1946835 , 3.12550771, 5.67275731, 1.0000195 , 1.82570239,5.62578391, 0.81923255, 2.00131474, 0.48190872, 4.78875363,5.60395833, 2.01674743, 2.13494958, 5.10829845, 0.95324309,1.59531506, 4.99145225, 6.19873491, 3.32802456, 1.15590926,0.52989939, 6.02205398, 3.66013508, 4.16276819, 2.60498467])

plt.figure(figsize=(10,10)) 


ax = plt.subplot(111, projection='polar')
ax.set_ylim(0,4)

ax.scatter(phi, rho, c=rho)

#phi.sort()
#rho.sort()

X, Y = np.meshgrid(phi, rho)

CS = ax.contourf(X, Y, Y, 2, alpha=0.4)

plt.show()

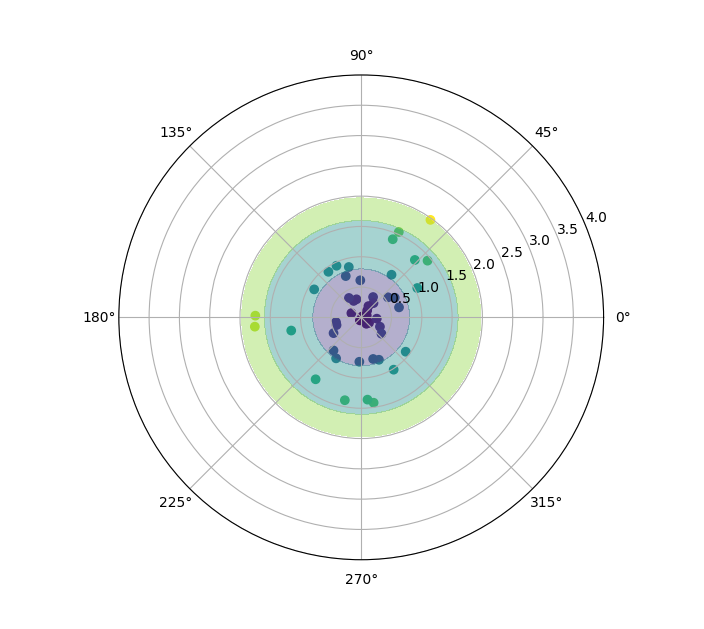
gives:

If you uncomment the sorting lines:

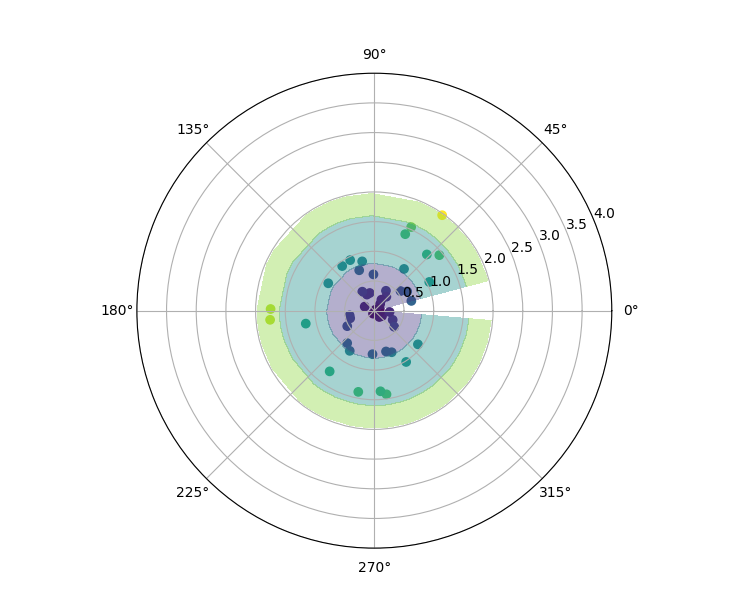
But now the contours look weird, because the base data does not the whole geometry of interest. So we can create same data just for the purpose of the filled contours, instead:

alfa = np.radians(np.linspace(0, 360, 60))
r = np.arange(0, np.max(rho) np.max(rho)/60, np.max(rho)/60)
r, alfa = np.meshgrid(r, alfa)
ax.contourf(alfa, r, r, 2, alpha=0.4)

Giving: