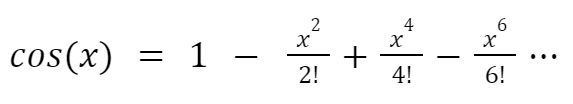Problems with precision loss in my cosine function-CodePudding

This is my task:

Write a C function to evaluate the series // cos(x) = x-(x2 /2!) (x4 /4!)-(x6 /6!) ... etc. Variable realNuber use radians instead of degrees

I lose precision, but I don't understand where. The answer with realNumber = 60 must be 0.500, but I've 0.501. Please help.

#include "stdio.h"
#include "inttypes.h"

double power(float N, uint32_t P){
    double buffer = 1;

    for (int i = 0; i < P;   i) {
        buffer *= N;
    }

    return buffer;
}

float factorial(float number){
    float result = number;

    if (number == 0) {
        return 0;
    }

    for (int i = 0; i < number - 1;   i) {
        result *= i   1;
    }

    return result;
}

float cos(float x){
    float result = x * (3.14159265359 / 180.);
    float polar = -1;

    for (int i = 2; i < 10; i  = 2) {
        result  = power(result, i) / factorial(i) * polar;
        polar *= -1;
    }

    return result;
}

int main(void){
    float realNumber = 0;
    float result = 0;

    scanf("%f", &realNumber);

    result = cos(realNumber);

    printf("%.13f", result);
}

I tried making changes in function cos(); maybe the problem is in a different place?

CodePudding user response：

You originally wrote:

Write a C function to evaluate the series // cos(x) = x-(x2 /2!) (x4 /4!)-(x6 /6!)

But that is NOT the Taylor series for cos.

The proper formula is:

(Note the 1 in the first term not an x)
Source

With a correction to your Taylor series, and some other fix up, I got:

Output

Success #stdin #stdout 0s 5392KB
0.4999999701977

My Code:

#include "stdio.h"
#include "inttypes.h"

// No Changes
double power(float N, uint32_t P){
    double buffer = 1;

    for (int i = 0; i < P;   i) {
        buffer *= N;
    }

    return buffer;
}

// No Changes
float factorial(float number){
    float result = number;

    if (number == 0) {
        return 0;
    }

    for (int i = 0; i < number - 1;   i) {
        result *= i   1;
    }

    return result;
}

// Minor changes, explained in comments
float cos(float x){
    x = x * (3.14159265359 / 180.); // Convert Degrees to Radians
    float result = 1;               // Taylor series starts with 1, not with x !!! 
    float polar = -1;

    for (int i = 2; i <= 10; i  = 2) {
        result  = power(x, i) / factorial(i) * polar;
        polar *= -1;
    }

    return result;
}

// Skipped the scanf in favor of hard-coded value, for simplicity.
int main(void){
    float realNumber = 60;
    float result = 0;

    result = cos(realNumber);

    printf("%.13f", result);
}

CodePudding user response：

Your cos function is plain wrong. The explanations are in the comments.

float cos(float x) {
  float anglerad = x * 3.14159265359 / 180; // multiply first, then divide, but 
                                            // it probably doesn't matter much here

  float result = 1;                         // initial result must be 1
  float sign = -1;                          // use proper naming

  for (int i = 2; i < 10; i  = 2) {
    // you need power(anglerad,.... not power(result,...)
    result  = power(anglerad, i) / factorial(i) * sign;

    sign *= -1;
  }

  return result;
}

The formula for cosine is 1-(x^2/2!) (x^4/4!) ...

You tried to use x-(x^2/2!) (x^4/4!) ... which is wrong.

Some general remarks:

althogh the corrected cos function is correct, it is not very efficient.

the repeated calls to the factorial function can be avoided, by using the result of the previous iteration. Remember: x! = x * (x-1)!. You even could use a table with hard coded values of the factorials from 2 to 10 (or some other upper bound if you want more iterations).
the repeated calls to the power function can be avoided. Remember: x^n = x * x^(n-1).
you could use more iterations.
you could use double instead of float.
and possibly a few more things.

CodePudding user response：

Small error in cos function. Try this.

float mycos(float x){
    float result = 1.0;
    float polar = -1;
    float xrad = x * (3.14159265359 / 180.);

    for (int i = 2; i < 10; i  = 2) {
        result  = power(xrad, i) / (factorial(i) * polar);
        polar *= -1;
    }

    return result;
}

CodePudding user response：

Here's how I would implement it in Java. The code should be similar enough to C for you to translate easily. No power or factorial calls needed. I hope you'll agree that it's much simpler.

public class TrigTaylorSeries {

    /**
     * Taylor series for cosine
     * @param x angle in radians
     * @param n terms to include (must be greater than zero)
     * @return cosine(x)
     * @link https://en.wikipedia.org/wiki/Taylor_series
     */
    public static double cos(double x, int n) {
        if (n <= 0) throw new IllegalArgumentException("Number of terms must be positive");
        double result = 0.0;
        double factor = 1.0;
        for (int i = 0; i < n;   i) {
            result  = factor;
            factor *= -x*x/(2*i 1)/(2*i 2);
        }
        return result;
    }
}

Here's a Junit test that shows it working correctly:

import org.junit.jupiter.api.Assertions;
import org.junit.jupiter.api.Test;

public class TrigTaylorSeriesTest {

    @Test
    public void testCosine() {
        // setup
        int nterms = 20;
        int npoints = 20;
        double t = 0.0;
        double dt = 2.0*Math.PI/npoints;
        double eps = 1.0e-9;
        // exercise
        // assert
        for (int i = 0; i < npoints 1;   i) {
            Assertions.assertEquals(Math.cos(t), TrigTaylorSeries.cos(t, nterms), eps, String.format("Incorrect result for %d", i));
            t  = dt;
        }
    }
}

Accurate to nine significant figures using 20 terms.