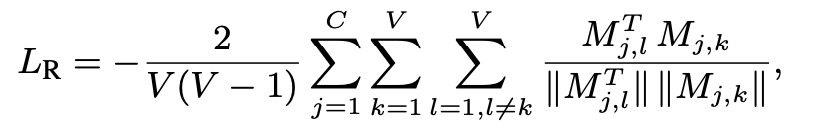In Tensorflow, how do I change a triple-nested loop into a parallelised tensor operation?-CodePudding

I'm trying to implement a loss function with the following formula:

For context, M is a 576 x 2 x 2048 matrix. C = 576 and V = 2.

Currently, my code is highly inefficient and is causing infeasible runtimes per epoch. I'm using a triple-nested for loop for this, which is probably why this is happening, but I'm not sure how one would write an operation that calculates cosine similarity between each and every channel of a matrix in this way?

Here's my naïve attempt at this:

        M = self.kernel

        norm_M = tf.norm(M, ord=2, axis=2)
        norm_X = tf.norm(X, ord=2, axis=1)

        # Compute reunion loss
        sum = 0.0
        for j in tf.range(C):
          for k in tf.range(V):
            for l in tf.range(V):
              if k == l:
                continue
              A = tf.tensordot(M[j][l], M[j][k], 1)
              B = norm_M[j][l] * norm_M[j][k]
              sum  = A / B
        l_r = -2/(self.V*(self.V-1)) * sum

CodePudding user response：

We need to create a mask to filter values at l != k, so that it doesnt come in the calculation.

M = np.random.randint(0,10, size=(5,8,7), dtype=np.int32).astype(np.float32)
norm_M = tf.linalg.norm(M, ord=2, axis=2)
mask = 1-tf.eye(M.shape[1]) #filter out the diagonal elements

A = tf.matmul(M, M, transpose_b=True)
B = tf.matmul(norm_M[...,None], norm_M[...,None], transpose_b=True)
C = (A/B)*mask
l_r = -2/(V*(V-1)) * tf.reduce_sum(C)