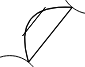
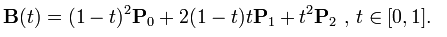I have a bezier curve and a line which intersects with the bezier curve (the one in the top left).

I am able to find the points at which the line intersects with the curve. I would like to find the tangent of the bezier curve at both of those point. I have a function which finds the tangent at a point t on the curve, though this t is a value between 0 and 1, rather than a coordinate. It looks like this:

let bezierCurveTangent = function(start: Point, end: Point, controlPoint: Point, t: number): Point {

    let x = 2 * (1 - t) * (controlPoint.x - start.x)   2 * t * (end.x - controlPoint.x);

    let y = 2 * (1 - t) * (controlPoint.y - start.y)   2 * t * (end.y - controlPoint.y);

    return { x, y };
}

How do I find the tangent for a point with x and y coordinates rather than a value for t?

The formula for a point on a bezier is curve looks like this:

Can I simply rearrange this equation for t, and then use that value in my function above?

There seems like there would be a better way of achieving this, rather than converting backwards and forwards between the value t and some point.

CodePudding user response：

Just search curve-line intersection in terms of t.

Having parametric equation of line (through points L0, L1)

L(u) = L0   (L1-L0)*u = L0   DL*u

we can write equation system

P0x*(1-t)^2 2*(1-t)*t*P1x t^2*P2x = L0x u*DLx
P0y*(1-t)^2 2*(1-t)*t*P1y t^2*P2y = L0y u*DLy

Express u from the first equation, substitute it in the second one,

u = (P0x*(1-t)^2 2*(1-t)*t*P1x t^2*P2x - L0x)/Dlx

substitute it in the second one,

(P0y*(1-t)^2 2*(1-t)*t*P1y t^2*P2y-L0y)*Dlx=
   (P0x*(1-t)^2 2*(1-t)*t*P1x t^2*P2x-L0x)*DLy

solve resulting quadratic eqiation, get t1 and t2 solutions (if they do exist and lie in 0..1 range)

CodePudding user response：

You could expand and solve the polynomials, but I believe there is a computationally simpler solution. Let P₀=(a₁,a₂), P₁=(b₁,b₂), P₂=(c₁,c₂). Let (x,y) be the point where you want to find the tangent.

1. First I want to move coordinates so that P₁ is the origin: let x=x' b₁, y=y' b₂. Now in the (x',y') coordinates the curve is given by

   B(t) = (1-t)²P₀ t² P₂

   After that the coordinates of P₀ and P₂ will be recalculated, I will use prime signs for them as well.

2. Then I want to rotate and scale the coodinate system in such a way that P₀ and P₂ move to points (0,1) and (1,0). This can be done by inverting the following matrix:

   

   Note that this always has an inverse if points P₀, P₁, P₂ don't lie on one line and it looks like this:

   

   So the new coordinates (x'',y'') are given by (x',y')=A(x'',y''). In this coordinate system the curve is given by

   B(t) = (1-t)²e₁ t²e₂

   Where e₁=(1,0) and e₂=(0,1). This simplifies to

   x''(t) = (1-t)²
   y''(t) = t²

If you know y'', it is trivial to find t=sqrt(y''). Note that the square root always exists (if you started with a point that lies on the bezier curve) since we changed coordinates in such a way that the curve lies where x>0 and y>0. And it is quite easy to find (x'',y'') knowing (x,y) from the formula (x'',y'')=(x c₁, y c₂)B. This is what it looks like

const getT = (start: Point, end: Point, controlPoint: Point, x: number, y: number) => {
  // xp stands for x'
  const xp = x - controlPoint.x
  const yp = y - controlPoint.y
  const a1p = start.x - controlPoint.x
  const a2p = start.y - controlPoint.y
  const c1p = end.x - controlPoint.x
  const c2p = end.y - controlPoint.y

  const det = a1p * c2p - a2p * c1p

  // This variable is redundant, but I left it for clarity
  const xpp = (xp * c2p - yp * c1p) / det
  const ypp = (- xp * a2p   yp * a1p) / det

  return Math.sqrt(ypp)
}

Or shorter

const getT = (start: Point, end: Point, controlPoint: Point, x: number, y: number) => Math.sqrt(
  (- (x - controlPoint.x) * (start.y - controlPoint.y) 
      (y - controlPoint.y) * (start.x - controlPoint.x)) / 
  ((start.x - controlPoint.x) * (end.y - controlPoint.y) -
    (start.y - controlPoint.y) * (end.x - controlPoint.x))
)