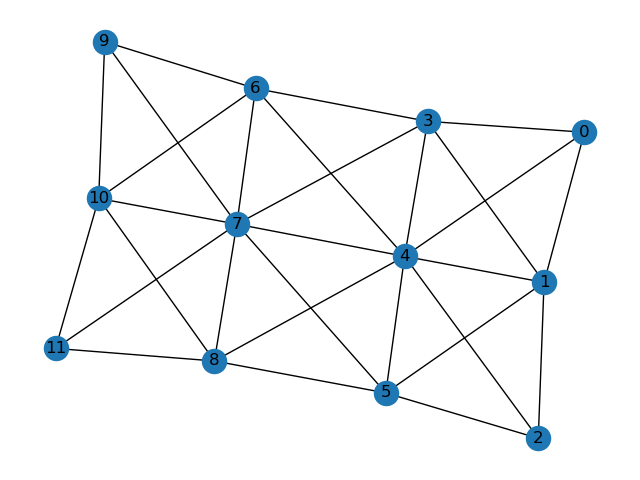
I need to connect these nodes in the pattern shown below:
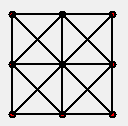
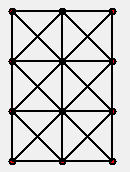
All of the nodes (circles) are stored in a list, I then have a 2d list which has pairs of numbers, these refer to the index of the nodes and show that there is a connection between them. To create the arrangement shown in the images, I have manually stored this list of connections in a variable.
I was hoping there was a way to take in this list of points and return this list of all of the point connections, which would work for any amount of points.
I tried to achieve by using itertools combinations:
connections=list(combinations(points, 2))
# draw combinations with lines between each point pair
Result:
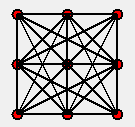
It gave me the wrong result, as you can see there are too many connections and it does not follow the pattern show in the above examples where I manually gave the connections.
CodePudding user response:
You need to specify the edges explicitly.
For every point at coordinates (i, j), there is a horizontal edge to the point to its east (i, j 1), a vertical edge to the point to its south (i 1, j), a diagonal edge to the point to its southeast (i 1, j 1), and a diagonal edge to the point to its northeast (i-1,j 1).
def grid(h, w):
vertices = [(i, j) for i in range(h) for j in range(w)]
edges = [((i,j), (i di, j dj))
for i in range(h-1) for j in range(w-1)
for (di, dj) in ((0, 1), (1, 0), (1, 1))]
edges.extend(((i,j), (i-1,j 1))
for i in range(1,h) for j in range(w-1))
edges.extend(((i, w-1), (i 1, w-1)) for i in range(h-1))
edges.extend(((h-1, j), (h-1, j 1)) for j in range(w-1))
return vertices, edges
def grid_with_simple_numbers_instead_of_pairs(h, w):
vertices, edges = grid(h, w)
vertices = [i * w j for (i, j) in vertices]
edges = [((i*w j), (k*w l)) for ((i,j), (k,l)) in edges]
return vertices, edges
## OR EQUIVALENTLY
def grid_with_simple_numbers(h, w):
vertices = list(range(h * w))
edges = [(i*w j, i*w j k)
for i in range(h-1) for j in range(w-1)
for k in (1, w, w 1)]
edges.extend((i*w j, (i-1)*w j 1)
for i in range(1,h) for j in range(w-1))
edges.extend((ij, ij w) for ij in range(w-1, h*w-1, w))
edges.extend((ij, ij 1) for ij in range((h-1)*w, h*w-1))
return vertices, edges
print(grid(2, 2))
# [(0, 0), (0, 1), (1, 0), (1, 1)],
# [((0, 0), (0, 1)), ((0, 0), (1, 0)), ((0, 0), (1, 1)), ((1, 0), (0, 1)), ((0, 1), (1, 1)), ((1, 0), (1, 1))]
print(grid_with_simple_numbers_instead_of_pairs(2, 2))
# [0, 1, 2, 3],
# [(0, 1), (0, 2), (0, 3), (2, 1), (1, 3), (2, 3)]
print(grid_with_simple_numbers(2, 2))
# [0, 1, 2, 3],
# [(0, 1), (0, 2), (0, 3), (2, 1), (1, 3), (2, 3)]
Testing:
import networkx as nx
import matplotlib.pyplot as plt
vertices, edges = grid_with_simple_numbers_instead_of_pairs(4, 3)
G = nx.Graph()
G.add_nodes_from(vertices)
G.add_edges_from(edges)
nx.draw(G, with_labels=True)
plt.show()
CodePudding user response:
The answer with explicit edges is already present.
On the other hand, you may not need to explicitly specify the edges — and nodes for that matter.
Consider the following approach.
A node is just a pair (row, col) with grid coordinates.
A connection is not stored anywhere: instead, for every node, its neighbors are generated on the fly.
Here is an example for your second picture:
deltas = [(-1, -1), (-1, 0), (-1, 1), ( 0, 1),
( 1, 1), ( 1, 0), ( 1, -1), ( 0, -1)]
rows = 3
cols = 2
def neighbors (row, col):
res = []
for dr, dc in deltas:
nr, nc = row dr, col dc
if 0 <= nr <= rows and 0 <= nc <= cols:
res.append ((nr, nc))
return res
for row in range (0, rows 1):
for col in range (0, cols 1):
print ((row, col), '->', neighbors (row, col))
And here are the neighbors it prints:
(0, 0) -> [(0, 1), (1, 1), (1, 0)]
(0, 1) -> [(0, 2), (1, 2), (1, 1), (1, 0), (0, 0)]
(0, 2) -> [(1, 2), (1, 1), (0, 1)]
(1, 0) -> [(0, 0), (0, 1), (1, 1), (2, 1), (2, 0)]
(1, 1) -> [(0, 0), (0, 1), (0, 2), (1, 2), (2, 2), (2, 1), (2, 0), (1, 0)]
(1, 2) -> [(0, 1), (0, 2), (2, 2), (2, 1), (1, 1)]
(2, 0) -> [(1, 0), (1, 1), (2, 1), (3, 1), (3, 0)]
(2, 1) -> [(1, 0), (1, 1), (1, 2), (2, 2), (3, 2), (3, 1), (3, 0), (2, 0)]
(2, 2) -> [(1, 1), (1, 2), (3, 2), (3, 1), (2, 1)]
(3, 0) -> [(2, 0), (2, 1), (3, 1)]
(3, 1) -> [(2, 0), (2, 1), (2, 2), (3, 2), (3, 0)]
(3, 2) -> [(2, 1), (2, 2), (3, 1)]
The point here is that there is often no need to store the connections when we can generate them on the fly every time we need them. The majority of graph algorithms (starting from BFS, DFS, and shortest paths) relies on the basic operation of the form "for every neighbor of this node, do that". This phrase can be replaced, in code, by:
... # "this node" is (row, col)
for dr, dc in deltas:
nr, nc = row dr, col dc
if 0 <= nr <= rows and 0 <= nc <= cols:
... # "do that" with node (nr, nc)
CodePudding user response:
As @luk2302 said, you can iterate through all the points and connect (x,y) to (x 1,y), (x,y 1), (x 1,y 1), and (x 1,y-1). Furthermore, if you want to store a list of connections between points I would suggest using an adjacency list implemented as a dictionary.
WIDTH = 2
LENGTH = 3
points = [(0, 0), (0, 1), (1, 0), (1, 1), (2, 0), (2, 1)]
connections = {}
for p in points:
connections[p] = []
for p in points:
if p[0] < LENGTH-1:
connections[p].append((p[0] 1, p[1]))
connections[(p[0] 1, p[1])].append(p)
if p[1] < WIDTH-1:
connections[p].append((p[0], p[1] 1))
connections[(p[0], p[1] 1)].append(p)
if p[0] > 0 and p[1] < WIDTH-1:
connections[p].append((p[0]-1, p[1] 1))
connections[(p[0]-1, p[1] 1)].append(p)
if p[0] < LENGTH-1 and p[1] < WIDTH-1:
connections[p].append((p[0] 1, p[1] 1))
connections[(p[0] 1, p[1] 1)].append(p)
What you end up with is a dictionary called connections, where connections[(x,y)] will return a list of all other tuples the point is connected to.
For example, connections[(0,0)] would return [(1,0), (0,1), (1,1)].
If you just want to draw the grid without doing any operations you can also remove the 2nd line of each 'if' statement.