Polyline path in 2D - find all nearest passing of landmark points-CodePudding

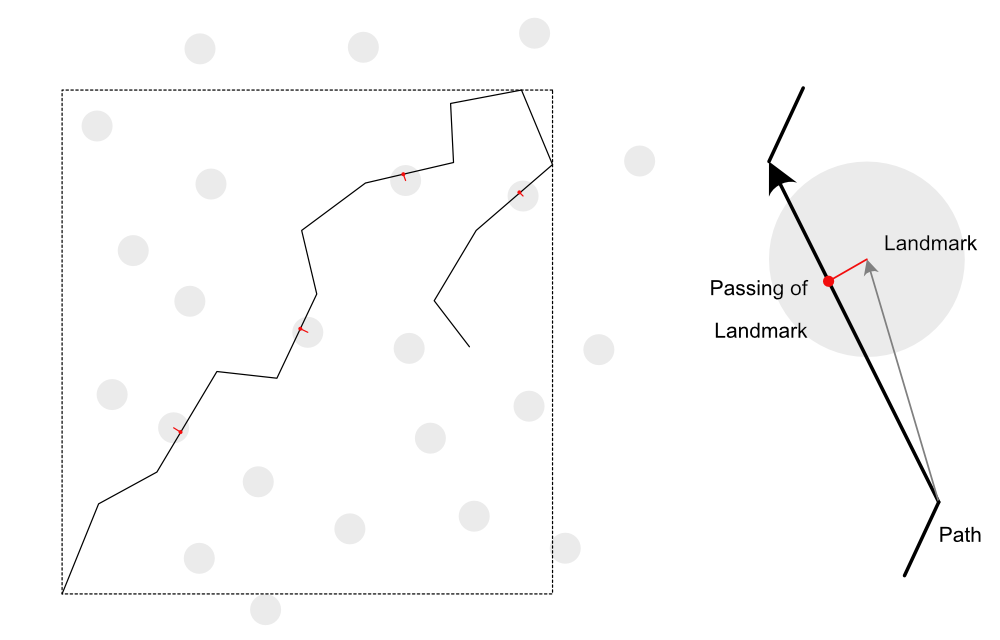
Given a poly-line path in 2D (like a GPS trace) I am interested in finding all points where the path gets close to existing landmarks. See the diagram below. This could be considered a problem Strava is solving when it reports running time between landmarks.

The landmarks have a small radius and I am only interested in them when the path crosses through that radius - finding the red dot where the paths is closest to the landmark.
There are many more landmarks than points on the paths.
Given a line segment and a landmark it is not difficult to compute the minimum distance using the vector dot product. The problem is to efficiently find the line segments that pass through landmarks.

I am not looking for code but the general algorithms and data structures to make this efficient - I lack the background in geometry where this problem is located.

The following properties could be exploited:

Using the bounding box of the path, the landmarks to be considered could be cut down. Landmarks could be stored in a quad-tree or 2d-tree for this.
The points of the paths form a sequence. One could walk along the paths only considering the next landmark that could come within reach.
Landmarks are static, paths change.

CodePudding user response：

The bird's eye view of multiple proximity data structures including quad- and 2d-trees is that you have a tree where

Each leaf has a site (here, a landmark point);
Each interior node has some data that gives a lower bound on the nearest site in its sub-tree.

The lower bound doesn't have to be the minimum; we could just use 0 everywhere (and thereby recover the brute force algorithm). This is the same idea as admissible heuristics in the A* algorithm.

Then to find all sites within some distance r of a query point, we traverse the tree but skip sub-trees where the lower bound is greater than r.

Thing is, this works for query line segments too (and many other geometric primitives besides). All we need is code to compute

The distance from a query primitive to a site,
A lower bound on the distance from a query primitive to sites in a sub-tree.

You already have the first. With quad- or 2d-trees, for the second, you could use a line-segment-to-box distance, or you could implement something simpler (e.g., maximum separation in either the horizontal or vertical dimension).