I've created this code and it gives me this error message:
Error using * Incorrect dimensions for matrix multiplication. Error in poli3 = sin(pi*a) ...
Below I show one function used in the code. I don't know if the problem comes from the value given by derivadan or what.
x = -1:0.01:1; % Intervalo en el que se evaluará el polinomio de Taylor
y = sin(pi*x); % Función
a = 0;
derivada3 = derivadan(0.01, 3, a);
derivada7 = derivadan(0.01, 7, a);
derivada3_vec = repmat(derivada3, size(x - a));
derivada7_vec = repmat(derivada7, size(x - a));
poli3 = sin(pi*a) derivada3_vec*(x - a) (derivada3_vec*(x - a).^2)/factorial(2) (derivada3_vec*(x - a).^3)/factorial(3);
poli7 = sin(pi*a) derivada7_vec*(x - a) (derivada7_vec*(x - a).^2)/factorial(2) (derivada7_vec*(x - a).^3)/factorial(3) (derivada7_vec*(x - a).^4)/factorial(4) (derivada7_vec*(x - a).^5)/factorial(5) (derivada7_vec*(x - a).^6)/factorial(6) (derivada7_vec*(x - a).^7)/factorial(7);
figure
plot(x, poli3, 'r', x, poli7, 'b')
legend('Taylor grau 3', 'Taylor grau 7')
title('Grafica Taylor 3 grau vs Grafica Taylor 7 grau')
function Yd = derivadan(h, grado, vecX)
Yd = zeros(size(vecX));
for i = 1:grado
Yd = (vecX(2:end) - vecX(1:end-1)) / h;
vecX = Yd;
end
end
CodePudding user response:
In MATLAB one can go 2 ways when developing taylor series; the hard way and the easy way.
As asked, first the HARD way :
close all;clear all;clc
dx=.01
x = -1 dx:dx:1-dx;
y = sin(pi*x);
a =0;
[va,na]=find(x==a)
n1=3
D3y=zeros(n1,numel(x));
for k=1:1:n1
D3y(k,1:end-k)=dn(dx,k,y);
end
T3=y(na) sum(1./factorial([1:n1])'.*D3y(:,na).*((x(1:end-n1)-a)'.^[1:n1])',1);
n2=7
D7y=zeros(n2,numel(x));
for k=1:1:n2
D7y(k,1:end-k)=dn(dx,k,y);
end
T7=y(na) sum([1./factorial([1:n2])]'.*D7y(:,na).*((x(1:end-n2)-a)'.^[1:n2])',1);
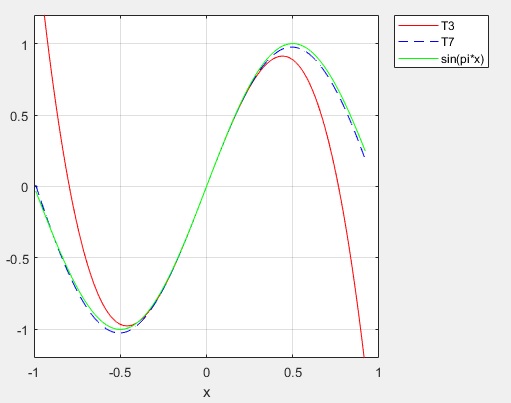
figure(1);ax=gca
plot(ax,x(1:numel(T7)),T3(1:numel(T7)),'r')
grid on;hold on
xlabel('x')
plot(ax,x(1:numel(T7)),T7(1:numel(T7)),'b--')
plot(ax,x(1:numel(T7)),y(1:numel(T7)),'g')
axis(ax,[-1 1 -1.2 1.2])
legend('T3', 'T7','sin(pi*x)','Location','northeastoutside')
the support function being
function Yd = dn(h, n, vecX)
Yd = zeros(size(vecX));
for i = 1:n
Yd = (vecX(2:end) - vecX(1:end-1))/h;
vecX = Yd;
end
end
Explanation
1.- The custom function derivadan that I call dn shortens one sample for every unit up in grado where grado is the derivative order.
For instance, the 3rd order derivative is going to be 3 samples shorter than the input function.
This causes product mismatch and when later on attempting plot it's going to cause plot error.
2.- To avoid such mismatchs ALL vectors shortened to the size of the shortest one.
x(1:end-a)
is a samples shorter than x and y and can be used as reference vector in plot.
3.- Call function derivadan (that I call dn) correctly
dn expects as 3rd input (3rd from left) a vector, the function values to differentiate, yet you are calling derivadan with a in 3rd input field. a is scalar and you have set it null. Fixed it.
derivada3 = derivadan(0.01, 3, a);
should be called
derivada3 = derivadan(0.01, 3, y);
same for derivada7
4.- So
error using * ...
error in poly3=sin(pi*a) ...
MATLAB doesn't particularly mean that there's an error right on sin(pi*a) , that could be, but it's not the case here >
MATLAB is saying : THERE'S AN ERROR IN LINE STARTING WITH
poly3=sin(pi*a) ..
MATLAB aborts there.
Same error is found in next line starting with
poly7 ..
Since sin(pi*a)=0 because a=0 yet all other terms in sum for poly3 are repmat outcomes with different sizes all sizes being different and >1 hence attempting product of different sizes.
Operator * requires all terms have same size.
5.- Syntax Error
derivada3_vec = repmat(derivada3, size(x - a))
is built is not correct
this line repeats size(x) times the nth order derivative !
it's a really long sequence.
Now the EASY way
6.- MATLAB already has command taylor
syms x;T3=taylor(sin(pi*x),x,0)
T3 = (pi^5*x^5)/120 - (pi^3*x^3)/6 pi*x
syms x;T3=taylor(sin(pi*x),x,0,'Order',3)
T3 = pi*x
syms x;T3=taylor(sin(pi*x),x,0,'Order',7)
T7 = (pi^5*x^5)/120 - (pi^3*x^3)/6 pi*x
T9=taylor(sin(pi*x),x,0,'Order',9)
T9 =- (pi^7*x^7)/5040 (pi^5*x^5)/120 - (pi^3*x^3)/6 pi*x
It really simplfies taylor series development because it readily generates all that is needed to such endeavour :
syms f(x)
f(x) = sin(pi*x);
a=0
T_default = taylor(f, x,'ExpansionPoint',a);
T8 = taylor(f, x, 'Order', 8,'ExpansionPoint',a);
T10 = taylor(f, x, 'Order', 10,'ExpansionPoint',a);
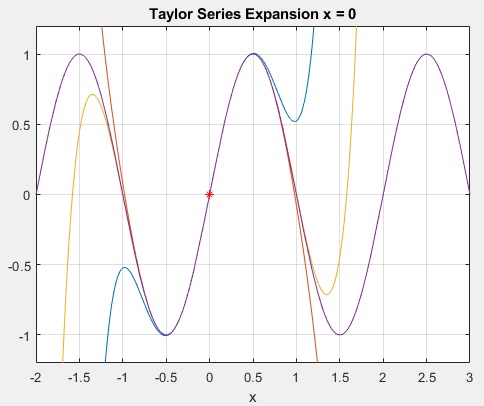
figure(2)
fplot([T_default T8 T10 f])
axis([-2 3 -1.2 1.2])
hold on
plot(a,f(a),'r*')
grid on;xlabel('x')
title(['Taylor Series Expansion x =' num2str(a)])
a=.5
T_default = taylor(f, x,'ExpansionPoint',a);
T8 = taylor(f, x, 'Order', 8,'ExpansionPoint',a);
T10 = taylor(f, x, 'Order', 10,'ExpansionPoint',a);
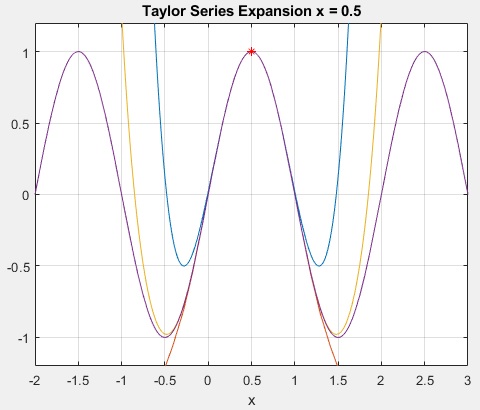
figure(3)
fplot([T_default T8 T10 f])
axis([-2 3 -1.2 1.2])
hold on
plot(a,f(a),'r*')
grid on;xlabel('x')
title(['Taylor Series Expansion x =' num2str(a)])
a=1
T_default = taylor(f, x,'ExpansionPoint',a);
T8 = taylor(f, x, 'Order', 8,'ExpansionPoint',a);
T10 = taylor(f, x, 'Order', 10,'ExpansionPoint',a);
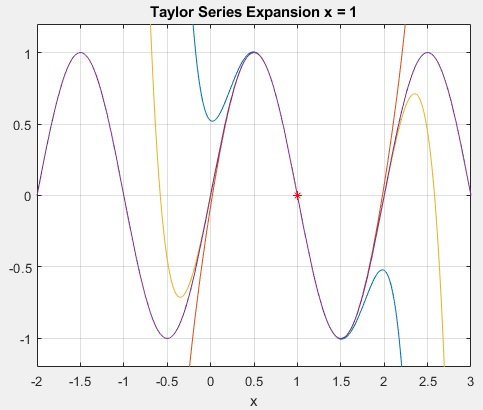
figure(4)
fplot([T_default T8 T10 f])
axis([-2 3 -1.2 1.2])
hold on
plot(a,f(a),'r*')
grid on;xlabel('x')
title(['Taylor Series Expansion x =' num2str(a)])
thanks for reading
CodePudding user response:
I checked the line that you were having issues with; it seems that the error is in the derivada3_vec*(x - a) (as well as in the other terms that use derivada3_vec).
Looking at the variable itself: derivada3_vec is an empty vector. Going back further, the derivada3 variable is also an empty vector.
Your issue is in your function derivadan. You're inputting a 1x1 vector (a = [0]), but the function assumes that a is at least 1x2 (or 2x1).
I suspect there are other issues, but this is the cause of your error message.