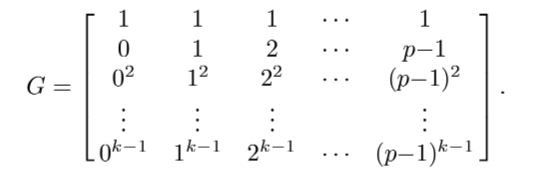How to efficiently create generator Matrix using Reed-Solomon encoding-CodePudding

I am coding a function to create generator matrix using Reed-Solomon encoding in Python. it is currently using for loops but i was wondering if there is a more efficient way to this. My code is:

def ReedSolomon(k,p):
    M = np.zeros((k,p))
    for i in range(k):
        for j in range(p):
            M[i][j] = j**i 
    return M

The encoding is:

I believe my function works but may not scale well to large p and k

CodePudding user response：

The generalized equation for an element at index r, c in your matrix is c**r.

For a matrix of shape k, p, you can create two aranges -- a row vector from 0 to p-1, and a column vector from 0 to k-1, and have numpy automatically broadcast the shapes:

def ReedSolomon(k,p):
    rr = np.arange(k).reshape((-1, 1))
    cc = np.arange(p)
    return cc**rr

Calling this function with e.g. k=5, p=3 gives:

>>> ReedSolomon(5, 3)
array([[ 1,  1,  1],
       [ 0,  1,  2],
       [ 0,  1,  4],
       [ 0,  1,  8],
       [ 0,  1, 16]])

CodePudding user response：

you can use numpy

p=5
k=7
A = np.arange(p).reshape((1,p))
A = np.repeat(A, k, axis=0)
B = np.arange(k).reshape((k,1))
B = np.repeat(B, p, axis=1)

M = A**B
print(M)
[[   1    1    1    1    1]
 [   0    1    2    3    4]
 [   0    1    4    9   16]
 [   0    1    8   27   64]
 [   0    1   16   81  256]
 [   0    1   32  243 1024]
 [   0    1   64  729 4096]]