I made a program to find all subsets of an array to length K. Im having trouble finding the time complexity of it, since the recursive call is within a for loop.

I think It's not theta, since the program can terminate, so I'm assuming Big O, but as far as time complexity - It's hard to tell. Any thoughts or guidance? Thanks!

myarr = [1,2,3]
k = 2
finalarr = []
def subsets(n, k):

    if k == len(n):
        if not n in finalarr:
            finalarr.append(n)
        return

    for i in n:
        aux = n[:]
        aux.remove(i)
        result = subsets(aux, k)

        if not result in finalarr and result:
            finalarr.append( result)

subsets(myarr, k)
print (finalarr)

CodePudding user response：

Optimal time complexity to find all subsets of an array - of a given length (k) is equal 2 to the power of k. The explanation is to consider every element of the array in two possible states: belongs or not belongs to a subset. The tricky thing is to remember about an empty set. Here's an example: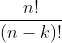

This could also be verified by plotting the call tree to the function subsets: first level consists of a single call, next level consists of n calls, then n-1 calls and so on until the last level which has n-k 1 calls. As the number of operations in the function subset (other than the recursive calls) is constant, we can simply multiply the number of calls in each level and get the aforementioned expression.

Two points to note:

1. This is not the most efficient algorithm, as each subset is produced several times. For example, the subset (1) of (1, 2, 3) can be produced either by first eliminating 2 and then eliminating 3 or vice versa.

2. The code contains the following condition:

   if not result in finalarr and result:
   
       finalarr.append( result)
   

   This condition is never satisfied as the function subset always returns None. These lines of code are thus redundant.