Density not suming to 1-CodePudding

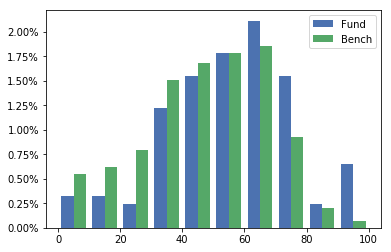
I am surprised to see that the probability density doesn't sum to 1. Is there a tweak to make it equal to 1?

import pandas as pd
import matplotlib.pyplot as plt
from matplotlib.ticker import PercentFormatter
plt.style.use('seaborn-deep')

#input file is a flat file that contains portfolio holdings and characteristics
input_file = r'\\CP\file.xls'

df = pd.read_excel(input_file,header=6)

#number of lines in Fund is 123
df_Fund=df[(df['Port. Weight']>0)]

#number of lines in Bench is 214
df_Bench=df[(df['Bench. Weight']>0)]

#Delta distribution
x = df_Fund['Delta']
y = df_Bench['Delta']

plt.hist([x,y],bins=10, density=True, range=(0,100), label=['Fund','Bench'])
plt.legend(loc='upper right')
plt.gca().yaxis.set_major_formatter(PercentFormatter(1))
plt.title='Delta Breakdown'
plt.show()

Graph:

screenshot of graph

CodePudding user response：

From the documentation

density bool, default: False

If True, draw and return a probability density: each bin will >display the bin's raw count divided by the total number of counts >and the bin width (density = counts / (sum(counts) * >np.diff(bins))), so that the area under the histogram integrates to >1 (np.sum(density * np.diff(bins)) == 1).

If stacked is also True, the sum of the histograms is normalized to 1.

The density is not also weighted by the bin width. As it looks like a binning of approximately 10, I would expect your data to sum to 0.1 instead of 1.

The way to interpret your graph is "For every x between 50 and 60 the probability is 1.75%"

So in order to "tweak" it to one, you either use a bin size of 1

bins=range(100)

or - as mentioned in the other answers - normalize your probabilities

CodePudding user response：

If you want it to sum to one, then you divide by the total sum.

For example if you are summing up some components and the sum to a number X

x_0   x_1   x_2   ... = X

so if you then it you divide each component by the total you get

(x_0/X)   (x_1/X)   (x_2/X)   ... = (x_0 x_1 x_2...)/X = X/X = 1

which is how you normalise any distribution (if the distribution is continuous then the sum becomes an integral)

hopefully that helps